Join Our Groups
TOPIC 5: THERMAL EXPANSION
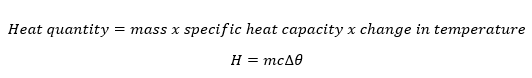
Thermal Energy
The Concept of Heat
Explain the concept of heat
Heat energy (thermal energy) is the form of energy that causes the vibration of the particles of a substance. The more the vibrations the more the heat energy contained.
Changes in the amount of heat energy contained in the substance cause changes in the temperature of the substance.
Temperature – Is the degree of hotness or coldness of a body.
SI Unit of Heat is Joule (J)
The amount of heat content depends on the mass of the body, specific heat capacity and the change in temperature and is mathematically obtained as;
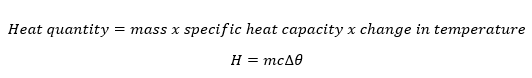
Source of Thermal Energy in Everyday Life
State the source of thermal energy in everyday life
There are numerous sources of energy such as the sun, fuels, nuclear sources, geothermal, electricity among others. The most important source of thermal energy is the sun. The sun generates its energy by a process called thermonuclear fusion. Most sources of thermal energy derive their energy from the sun. Thermal energy from the sun makes life on earth possible.
Difference between Heat and Temperature
Distinguish between heat and temperature
Heat and temperature are related and often confused. More heat usually means a higher temperature.
Heatis energy. It is the total amount of energy (both kinetic and potential) possessed by the molecules in a piece of matter. Heat is measured in Joules.
Temperatureis not energy. It relates to the average (kinetic) energy of microscopic motions of a single particle in the system per degree of freedom. It is measured in Kelvin (K), Celsius (C) or Fahrenheit (F).
When you heat a substance, either of two things can happen: the temperature of the substance can rise or the state of substance can change.
| Heat | Temperature | |
|---|---|---|
| Definition | Heat is energy that is transferred from one body to another as the result of a difference in temperature. | Temperature is a measure of hotness or coldness expressed in terms of any of several arbitrary scales like Celsius and Fahrenheit. |
| Symbol | Q | T |
| Unit | Joules | Kelvin, Celsius or Fahrenheit |
| SI unit | Joule | Kelvin |
| Particles | Heat is a measure of how many atoms there are in a substance multiplied by how much energy each atom possesses. | Temperature is related to how fast the atoms within a substance are moving. The ‘temperature’ of an object is like the water level – it determines the direction in which ‘heat’ will flow. |
| Ability to do work | Heat has the ability to do work. | Temperature can only be used to measure the degree of hea |
Thermal Expansion of Solids
Expansion of Solids
Demonstrate expansion of solids
When a solid is heated one or more of the following may occur:
- Its temperature may rise
- Its state may change
- It may expand
Expansion of solids is the increase in dimensions of a solid when heated.
Contraction of solids is the decrease in dimensions of a solid when is cooled.
Cooling is simply the process of removing heat from the substance.
DEMONSTRATION OF EXPANSION OF SOLIDS
In order to demonstrate the expansion of solid we can use following method
- The ball and Ring Experiment
- The Bar and Gap Experiment
Here we are going to explain about the Ball and Ring experiment.
The Ball and Ring Experiment
1st Case: When the ball is not heated then it will pass through the ring very easily because it has a small volume.

2nd Case: When the ball is heated, it will expand and increase in volume, so it will not pass through the ring.

The Bar and Gap experiment
1stCase:When the Bar not heated (Not raised with temperature) then the dimension will remain constant.
2nd Case:When the Bar is heated (raised with temperature) then the dimension of the Bar will increase and eventually will not pass thought the Gap.
Expansion of Solids in terms of Kinetic Theory of Matter
Explain expansion of solids in terms of kinetic theory of matter
When asolidis heated, its atoms vibrate faster about their fixed points. The relative increase in the size of solids when heated is therefore small. Metal railway tracks have small gaps so that when the sun heats them, the tracks expand into these gaps and don’t buckle.
Forces due toexpansion
Normally Expansion and contraction is accompanied by tremendous forces; The presence of force indicates the expansion and contraction is resisted.

Bar breaker
- Consists a strong metal blocker with a pair of vertical jaws J and a strong metal Bar R. The metal bar has a wing nut N at one end and an eye at the other end.
- The bar is placed between the two pair of Jaws
- A short cast iron C is inserted in the eye of the bar.
- The bar is then heated it expands and the wing not screwed to tighten the bar R against the jaws.
- The bar is then allowed to cool as it cools, it contracts the short cast Iron rod C which presses against the jaws of the bar breaker, Resists the contraction of the Metal bar R.
- The resistance to the contraction of the bar sets up very large forces which breaks the short cast Iron rod C in the eye of metal bar, Because the contracting bar is trying to pull itself through the small gap in the frame.
Expansivity of Different Solids
Identify expansivity of different solids
The coefficient of linear expansion or linear expansivity
The amount by which the linear dimension of a given solid expands depends on:
- The length of the solid
- The temperature to which the solid is heated
- The nature of solid
Coefficient of linear Expansivity is the fractional increase in length of the solids per original length per degree rise in temperature.
Mathematical formula

SI Unit of coefficient of linear expansion is per degree centigrade (ºC-1) or per Kelvin (K-1).
Example 1
A copper rod has a length of 40cm on a day when the temperature of the room is 22.3ºC. What will be its length become on a day when the temperature of the room is 30ºC ? The linear expansivity of copper is 0. 000017/ºC
Solution
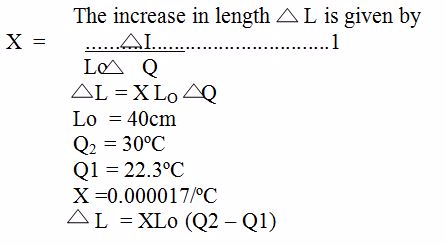
Table which shows the coefficient of Expansivity Constant.
| Substance | Linear Expasivity (PerºC) |
| Aluminum (Al) | 0.000026 |
| Brass | 0.000019 |
| Copper | 0.000017 |
| Iron | 0.000012 |
| Steel | 0.000012 |
| Concrete | 0.000011 |
| Glass | 0.0000085 |
| Invar ( Alloy of Iron and Nickel) | 0.000001 |
The Application of Expansion of Solids in Daily Life
Explain the applications of expansion of solids in daily life
There is a large number of important practical applications of thermal expansion of solids; While laying the railway tracks, a small gap is left between the successive lengths of the rails. This will allow expansion during a hot day. The iron tyre is to be put on a wheel, the tyre is first heated until its diameter becomes more than that of the wheel and is then slipped over the wheel.
Thermal Expansion of Liquids
The Apparent Expansion of Liquids
Explain the apparent expansion of liquids
Liquids expands when heated and contracts when cooled. It is easier to observe expansion in liquids than in solids. Different liquids expand at different rates in response to the same temperature change. Liquids expand much more than solids for equal changes of temperature. Apparent expansion of liquids is always less than the true expansion of the liquid.
Demonstrate the Effects of Heat on Liquids
Demonstrate the effect of heat on liquids
Liquids unlike solids can be poured. If a liquid is poured into a vessel, it takes the shape of the vessel. For this reason a liquid can't have linear and aerial expansivity, thus liquids have only volume expansivity. Liquids molecules have kinetic energy. This energy increases if the temperature of the liquid is raised by heating. Heating causes the molecules of liquid to move faster.
Activity 1
Items Needed
- Large heat safe glass bowl
- Cooking Oil
- Food Coloring
- Two 2×4 blocks
- Candle
- Match or Lighter
Instructions
- Begin by filling a large glass bowl with cooking oil.
- Next, add between 5-10 drops of food coloring into the oil. Helpful Tip: Place the drops near the center of the bowl.
- Prop the bowl up off the table using two 2×4 blocks.
- Light a candle and carefully place it under the bowl. The flame of the candle should touch the bottom of the glass bowl.
- Look through the side of the glass bowl and watch carefully to observe what happens. Helpful Tip: It will likely take 5 minutes before you see anything happen to the liquid/food coloring.
You can alternatively follow the experiment through the following vedio
Verification of Anomalous of Water
Verify the anomalous expansion of water
The instrument used to demonstrate anomalous expansion of water is called Hope's apparatus. It consists of a brass cylinder, jacket with a mixture of ice and salt and two thermometers at regular intervals upward and at the bottom. The Hope's experiment shows that water contracts as it cools down to 40C and then expands as it cooled further below 40C.
In the year 1805, the scientist T. C. Hope devised a simple arrangement, known as Hope’s apparatus, to demonstrate the anomalous behaviour of water.
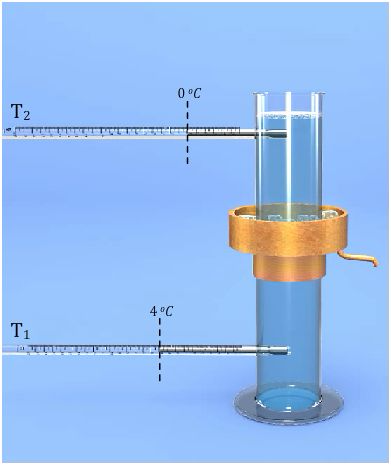
Hope’s apparatus consists of a long cylindrical jar with two openings on the side, one near the top and the other near the bottom to fit thermometers in each of these openings. A metallic cylindrical air-tight trough with an outlet is also fitted onto the jar, on its central portion. Two thermometers are fitted air-tight in the two openings of the cylindrical jar. The thermometer near the bottom of the jar is T1, and the one near the top of the jar is T2. Now the cylindrical jar is filled with water. The cylindrical trough at the central portion of the jar is filled with a freezing mixture of ice and common salt.
The Application of Expansion of Liquids in Everyday Life
Explain the applications of expansion of liquids in everyday life
Water in lakes and ponds usually freezes in winter. Ice, being less dense floats on the water. This insulates the water below against heat loss to the cold air above. Water at 4 degree centigrade being most dense, remains at the bottom of the lake, while ice, being less dense than water floats on the layers of water. This enables aquatic animals to survive in the water below the ice.
Thermal Expansion of Gases
The Concept of Thermal Expansion of Gases
Explain the concept of thermal expansion of gases
Gases expand when heated just like solids and liquids. This is because the average kinetic energy of the molecules in a gas is directly proportional to the absolute temperature of the gas. Heating the gas increases the kinetic energy of its molecules, making them vibrate more vigorously and occupy more space.
The Relationship between Volume and Temperature of Fixed Mass of Air at Constant Pressure
Investigate the relationship between volume and temperature of fixed mass of air at constant pressure
Three properties are important when studying the expansion of gases. These are; pressure, volume and temperature. Charles' law states that "the volume of a fixed mass of gas is directly proportional to the absolute (Kelvin) temperature provided the pressure remains constant." Mathematically, V1T2= V2T1.
Example 2
The volume of gas at the start is recorded as 30cm3 with a temperature of 30°C. The cylinder is heated further till the thermometer records 60°C. What is the volume of gas?
Solution:
We know,V/T = constant
therefore,
V1/T1=V2/T2
V1 =30 cm3
T1 =30°C = 30+273 = 303K(remember to convert from Celsius to Kelvin)
T2 =60°C = 60+273 = 333K
V2 =?
V1/T1=V2/T2
V2=V1xT2/T1
V2=30x333/303
= 32.97 cm3
The Relationship between Pressure and Volume of a Fixed Mass of Air at Constant Temperature
Investigate the relationship between pressure and volume of a fixed mass of air at constant temperature
The relationship obtained when the temperature of a gas is held constant while the volume and pressure are varied is known as Boyle’s law. Mathematically, P1V1= P2V2. Boyle's law states that the volume of a fixed mass of gas is inversely proportional to its pressure if the temperature is kept constant.
PressurexVolume = constant
PxV = constant
Example 3
The volume of gas at the start is 50 cm3with a pressure of 1.2 x 105Pascals. The piston is pushed slowly into the syringe until the pressure on the gauge reads 2.0 x 105Pascals. What is the volume of gas?
Solution:
We know
P x V = constant
Therefore,
P1xV1=P2xV2
P1=1.2 x 105Pascals
V1=50 cm3
P2=2.0 x 105Pascals
V2=?
P1 xV1=P2 xV2
V2=P1xV1/p2
V2=(1.2x105x50)/(2.0 x 105)
V2= 30 cm3
The Relationship between Pressure and Temperature of a Fixed Mass of Air at Constant Volume
Investigate the relationship between pressure and temperature of a fixed mass of air at constant volume
To investigate the relationship between the pressure and the temperature of a fixed mass, the volume of the gas is kept constant. The pressure is then measured as the temperature is varied. P1/T1 = P2/T2 ,this is called pressure law. The pressure law states that "the pressure of a fixed mass of a gas is directly proportional to the absolute temperature if the volume is kept constant".
Example 4
Pressure of gas is recorded as 1.0 x 105N/m2at a temperature of 0°C. The cylinder is heated further till the thermometer records 150°C. What is the pressure of the gas?
Solution:
We know, P/T = constant
Therefore,
P1 /T1=P2/T2
P1 =1.0 x 105N/m2
T1=0°C = 0+273 = 273K(remember to convert from Celsius to Kelvin)
T2=150°C = 150+273 = 423K
P2 =?
P1/T1 = P2/T2
p2=p1xT2/T1
p2=1.0x105x423/273
= 1.54 x 105N/m2
The General Gas Equation from the Gas Laws
Identify the general gas equation from the gas laws
The three gas laws give the following equations:
- pV = constant (when T is kept constant)
- V/T = constant (when p is kept constant)
- P/T= constant (when V is kept constant)
These 3 equations are combined to give the ideal gas equation:
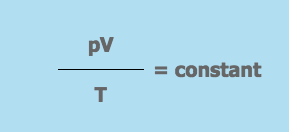
Where,
- p = the pressure of the gas
- V = the volume the gas occupies
- T = the gas temperature on the Kelvin scale
From this equation we know that if a fix mass of gas has starting values of p1, V1 and T1, and then some time later has value p2, V2 and T2, the equation can be written as:
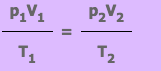
Exercise 1
Sabah pumps up her front bicycle tyre to 1.7 x 105Pa. The volume of air in the tyre at this pressure is 300 cm3. She takes her bike for a long ride during which the temperature of the air in the tyre increases from 20°C to 30°C. Calculate the new front tyre pressure assuming the tyre had no leaks and so the volume remained constant?
Absolute Scale of Temperature
Explain absolute scale of temperature
Absolute zero is the lowest temperature that can be attained theoretically. It is not possible to attain this temperature because all gases liquefy before attaining it. The Kelvin scale of temperature is obtained by shifting the vertical axis to -273 degrees Celsius and renaming it 0 K. On the scale 0 degrees Celsius becomes 273 K and 100 degrees Celsius corresponds with 373 K.
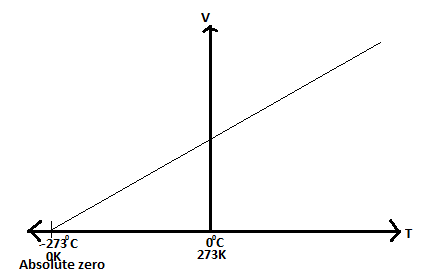
Convertion of Temperature in Degrees Centigrade (Celsius) to Kelvin
Convert temperature in degrees centigrade (celsius) to kelvin
The Kelvin temperature scale takes its name after Lord Kelvin who developed it in the mid 1800s. It takes absolute zero as the starting point and temperature measurements are given the symbol K (which stands for "Kelvin"). Temperature differences on the Kelvin scale are no different to those on the Celsius (°C) scale. The two scales differ in their starting points. Thus, 0°C is 273K.
Converting from Celsius to Kelvin
- Temperature in °C + 273 = Temperature in K
Converting from Kelvin to Celsius
- Temperature in K – 273 = Temperature in °C
Example 5
The temperature of a gas is 65 degrees Celsius. Change it to the kelvin scale.
Solution
T(K) = degrees Celsius + 273, T(K) = 65+273
therefore T(K) = 338 K.
Standard Temperature and Pressure (S.T.P)
Explain standard temperature and pressure (S.T.P)
The standard temperature and pressure (S.T.P) is a set of conditions for experimental measurements to enable comparisons to be made between sets of data. The standard temperature is 0 degrees Celsius (273 K) while the standard pressure is 1 atmosphere (101300 Pa or 760 mm of mercury).
Expansion of Gas in Daily Life
Apply expansion of gas in daily life
Land and sea breezes are the result of expansion of air caused by unequal heating and cooling of adjacent land and sea surfaces. The piston engine and firing bullets from guns work under principles of expansion of gases.







Exellent
ReplyDelete