Join Our Groups
TOPIC 2: ALGEBRA
When we play games with computers we play by running, jumping and or finding secret things. Well, with Algebra we play with letters, numbers and symbols. And we also get to find secret things. Once we learn some of the ‘tricks’ it becomes a fun challenge to work with our skills in solving each puzzle. So, Algebra is all about solving puzzles. In this chapter we are going to learn some of the skills that help in solving mathematics puzzles.
Binary Operations
The Binary Operations
Describe the binary operations
When two numbers are combined according to the instructions given and produce one number we say that they are binary operations. For example, when we add 4 to 6 we get 10, or when we multiply 4 by 3 we get 12. We see that addition of two numbers lead to one number and multiplication of two numbers produce one number. This is binary operation. The instructions can be given either by symbols like X,*,∇and so on or by words.
Performing Binary Operations
Perform binary operations
Example 1
Evaluate:

solution
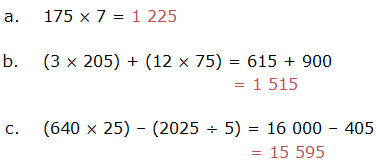
Example 2
Find
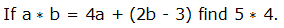
solution

Example 3
Solve
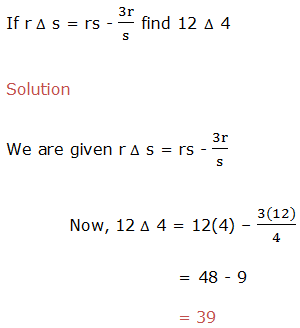
Example 4
evaluate,
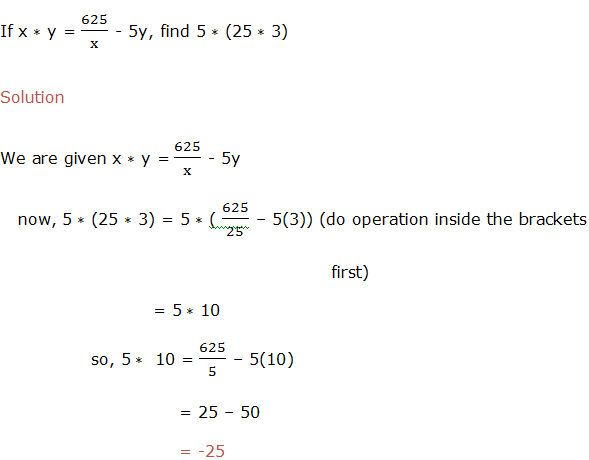
Example 5
Calculate
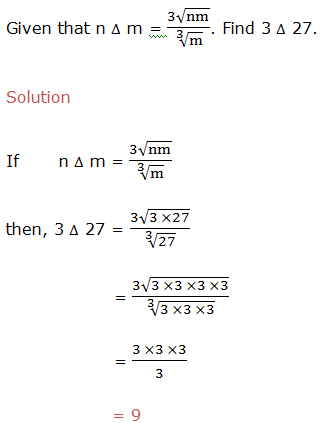
Brackets in Computation
Brackets are used to group items into brackets and these items inside the brackets are considered as whole. For example,15 ÷(X + 2) ,means that x and 2 are added first and their sum should divide 15. If we are given expression with mixed operations, the following order is used to perform the operations: Brackets (B) are opened (O) first followed by Division (D) then Multiplication (M), Addition (A) and lastly Subtraction (S). Shortly is written as BODMAS.
Basic Operations Involving Brackets
Perform basic operations involving brackets
Example 6
Simplify the following expressions:
- 4 + 2b – (9b ÷3b)
- 4z – (2x + z)
solution

Algebraic Expressions Involving the Basic Operations and Brackets
Simplify algebraic expressions involving the basic operations and brackets
Example 7
Evaluate the following expressions:
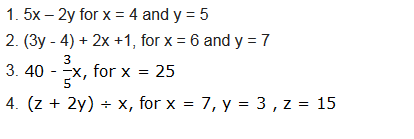
solution
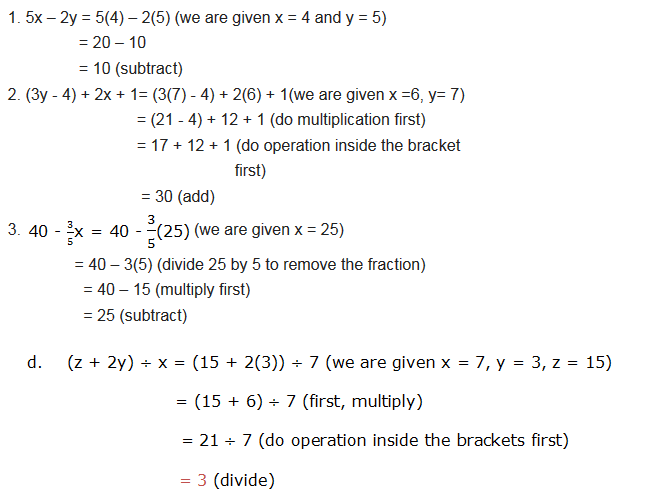
Identities
For example, 3(2y + 3) = 6y + 9, when y = 1, the right hand side (RHS) and the left hand side (LHS) are both equals to 15. If we substitute any other, we obtain the same value on both sides. Therefore the equations which are true for all values of the variables on both sides are called Identities. We can determine whether an equation is an identity or not by showing that an expression on one side is identical to the other expression on the other side.
Example 8
Determine whether or not the following expressions are identities:
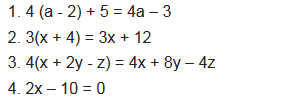
solution


Quadratic Expressions
A Quadratic Expression from Two Linear Factors
Form a quadratic expression from two linear factors
A quadratic expression is an expression where the highest exponent of the variable (usually x) is a square (x2). It is usually written as ax2+bx+c.
Activity 1
Quadratic expression from two linear factors
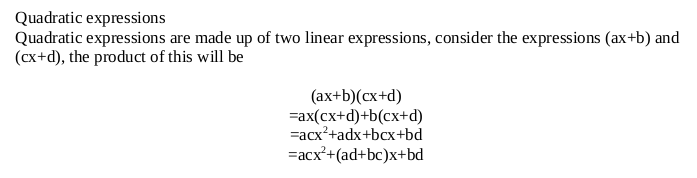
The General Form of Quadratic Expression
Write the general form of quadratic expression
Quadratic expression has the general form of ax2 + bx + c where a ≠ 0 and a is a coefficient of x2 , b is a coefficient of x and c is a constant. its highest power of variable is 2. Examples of quadratic expressions are 2x2 + x + 1, 4y2 + 3, 3z2 – 4z + 1 and so on. In a quadratic expression 3z2 - 4z + 1, a = 3, b = -4 and c = 1. Also in quadratic expression 4y2 + 3, a = 4, b = 0 and c = 3
Example 9
If you are told to find the area of a rectangle with a length of 4y + 3 and a width of 2y + 1.
Solution


Example 10
3x items were bought and each item costs (4x – 3) shillings. Find total amount of money used.

Factorization
Linear Expressions
Factorize linear expressions
The operation of resolving a quantity into factors, when we expand expressions, is done by removing the brackets. The reverse operation is Factorizing and it is done by adding brackets.
Example 11
Factorize the expression 5a+5b.
Solution
In factorization of 5a+5b, we have to find out a common thing in both terms. We can see that the expression 5a+5b, have got common coefficient in both terms, that is 5. So factoring it out we get 5(a+b).
Example 12
Factorize 18xyz-24xwz
Solution
Factorizing 18xyz-24xwz, we have to find out highest common factor of both terms. Then factor it out, the answer will be 9xz(2y-3w).
Quadratic Expressions
Factorize quadratic expressions
When we write the quadratic expression as a product of two factors we say that we have factorized the expression. We are going to learn two methods used to factorize quadratic expressions. These methods are factorization by Splitting the middle term and factorization by Inspection.
Factorization by splitting the middle term

Example 13
factorize 3x2 - 2x – 8 by splitting the middle term.
Solution

Example 14
factorize x2 + 10x + 25 by splitting the middle term.

Factorization by Inspection
Example 15
factorize x2 + 3x + 2 by inspection.

Example 16
factorize 4x2 + 5x – 6 by inspection.

Exercise 1
Factorization Exercise;








EmoticonEmoticon