MATHEMATICS: FORM TWO: Topic 3 - QUADRATIC EQUATIONS

 Join Our Groups

TELEGRAM | WHATSAPP

Schemes of Work 2024

Necta Timetables 2024

English Course - Free

Kenya Notes

TOPIC 3: QUADRATIC EQUATIONS

Solving quadratic equations can be difficult, but luckily there are several different methods that we can use depending on what type of quadratic that we are trying to solve. The four methods of solving a quadratic equation are factoring, using the square roots, completing the square and the quadratic formula.

Solving Equations

The standard form of a Quadratic equation is ax² + bx + c =0 whereby a, b, c are known values and ‘a’ can’t be 0. ‘x’ is a variable (we don’t know it yet). a is the coefficient of x² , b is the coefficient of x and cis a constant term. Quadratic equation is also called an equation of degree 2 (because of the 2 on x). There are several methods which are used to find the value of x. These methods are:

1. by Factorization
2. by completing the square
3. by using quadratic formula

The Solution of a Quadratic Equation by Factorization

Determine the solution of a quadratic equation by factorization

We can use any of the methods of factorization we learnt in previous chapter. But for simplest we will factorize by splitting the middle term. For Example: solve for x, x² + 4x = 0

solution

Since the constant term is 0 we can take out x as a common factor.

So, x² + 4x = x(x + 4) = 0. This means the product of x and (x + 4) is 0. Then, either x = 0 or x + 4 = 0. If x + 4 = 0 that is x = -4. Therefore the solution is x = 0 or x = -4.

Example 1

Solve the equation: 3x² =- 6x – 3.

first rearrange the equation in its usual form.

that is:

3x² = - 6x – 3

3x² + 6x + 3 = 0

now, factorize the equation by splitting the middle term. Let us find two numbers whose product is 9

and their sum is 6. The numbers are 3 and 3. Hence the equation 3x² + 6x + 3 = 0 can be written as:

3x² + 3x + 3x + 3 = 0

3x(x + 1) + 3(x + 1) = 0

(3x + 3)(x + 1) (take out common factor which is (x + 1))

either (3x + 3) = 0 or (x + 1) = 0

therefore 3x = -3 or x = -1

x = -1 (divide by 3 both sides) or x = -1

Therefore, since the values of x are identical then x = -1.

Example 2

solve the equation 10 – 3y - 1 = 0 by factorization.

Solution

Two numbers whose product is -10 and their sum is -3 are 2 and -5.

Then, we can write the equation 10y² – 3y - 1 = 0 as:

2y(5y + 1) – 1(5y + 1) = 0

(2y – 1)(5y + 1) = 0

Therefore, either 2y – 1 = 0 or 5y + 1 = 0

Example 3

solve the following quadratic equation by factorization: 4x² - 20x + 25 = 0.

Solution

We need to split the middle term by the two numbers whose product is 100 and their sum is -20. The numbers are -10 and -10.

The equation can be written as:

4x² -10x - 10x + 25 = 0

2x(2x - 5) – 5(2x -5) = 0

(2x – 5)(2x - 5) (take out common factor. The resulting factors are identical. This is a perfect square)

since it is a perfect square, then we take one factor and equate it to 0. That is:

2x – 5 = 0

2x = 5 then, divide by 2 both sides.

Therefore

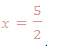
Example 4

solve the equation x² - 16 = 0.

Solution

We can write the equation as x² - 4² = 0. This is a difference of two squares. The difference of two squares is an identity of the form:

a² - b² = (a - b)(a + b).

So, x² - 4² = (x - 4)(x + 4) = 0

Now, either x- 4 = 0 or x + 4 = 0

Therefore x = 4 or x = -4

The Solution of a Quadratic Equation by Completing the Square

Find the solution of a quadratic equation by completing the square

Completing the square.

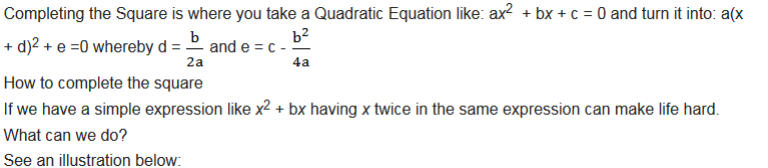
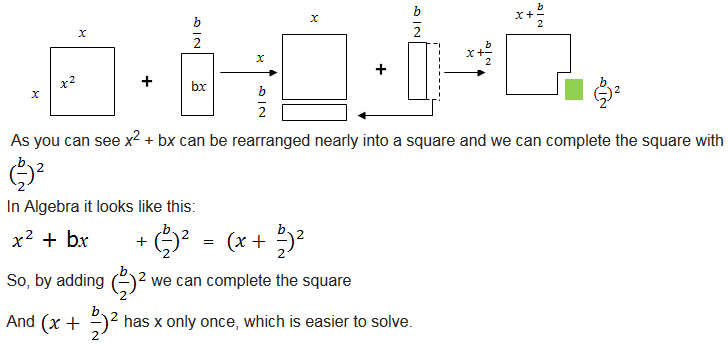
Example 5

Add a term that will make the following expression a perfect square: x² - 8x

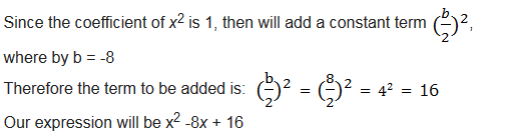
find a term that must be added to make the following expression a perfect square: x² + 10x

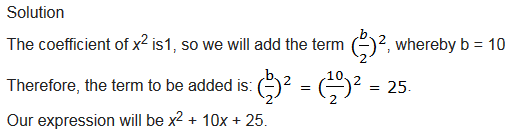
Example 6

solve the following quadratic equation by completing the square: x² + 4x + 1 = 0

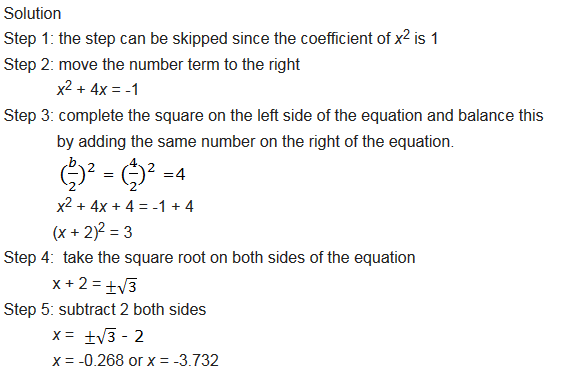
Example 7

solve by completing the square: 3x² + 7x – 6 = 0

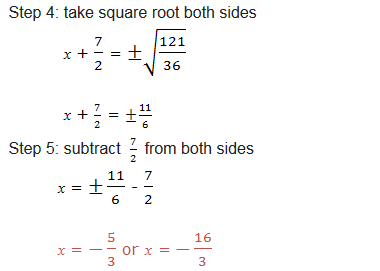
General Solution of Quadratic Equations

The Quadratic Formula

Derive the quadratic formula

The special quadratic formula used for solving quadratic equation is:

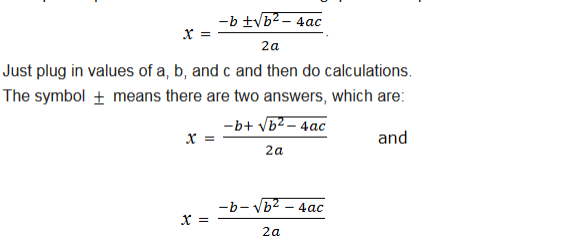
Quadratic Equations using Quadratic Formula

Solve quadratic equations using quadratic formula

Example 8

solve 5x² – 8x + 3 = 0 by using quadratic formula.

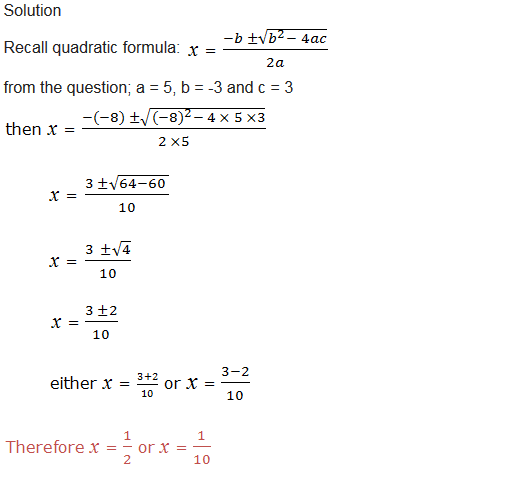
Example 9

solve this quadratic equation by using quadratic formula: 3x² = - 7x - 4

Word problems leading to quadratic equations

Given a word problem; the following steps are to be used to recognize the type of equation.

Step1: choose the variables to represent the information

Step 2: formulate the equation according to the information given

Step 3: solve the equation by using any of the method you know

In order to be sure with your answers, check if the solution you obtained is correct.

Example 10

the length of a rectangular plot is 8 centimeters more than the width. If the area of a plot is 240cm², find the dimensions of length and width.

Solution

Let the width be x

The length of a plot is 8 more than the width, so the length of a plot be x + 8

We are given the area of a plot = 240cm² and the area of a rectangle is given by length ×width

then (x + 8) × x = 240

x² + 8x = 240

rearrange the equation

x² + 8x – 240 = 0

then solve the equation to find the value of x

Solving by splitting the middle term, two numbers whose product is -240 and their sum is 8, the number

are -12 and 20

our equation becomes; x² + 20x – 12x – 240 = 0

x(x + 20) – 12(x + 20) = 0

either (x - 12) = 0 or (x + 20) = 0

x = 12 or x = -20

since we don’t have negative dimensions, then the width is 12cm and the length is 12 + 8 = 20cm

Therefore the rectangular plot has the length of 20cm and the width of 12cm.

Example 11

A piece of wire 40cm long is cut into two parts and each part is then bent into a square. If the sum of the areas of these squares is 68 square centimeters, find the lengths of the two pieces of wire.

Exercise 1

1. Solve each of the following quadratic equations by using factorization method:

1. -6x²+ 23x – 20 = 0
2. X²– x -12 = 0

2. Solve these equations by completing the square: