Join Our Groups
TOPIC 1: EXPONENTS AND RADICALS


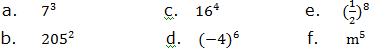
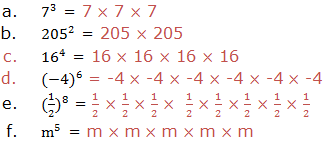
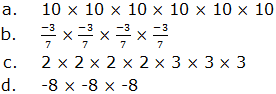
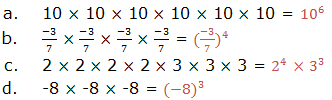
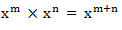
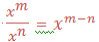
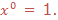
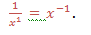
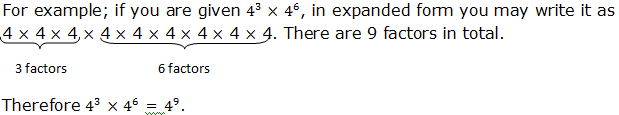
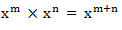
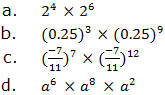
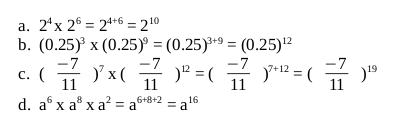
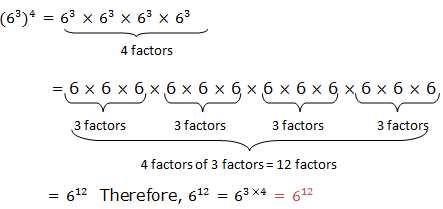
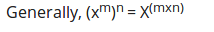
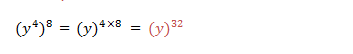
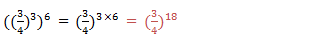
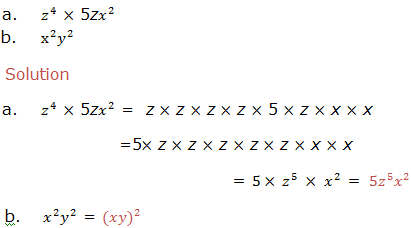
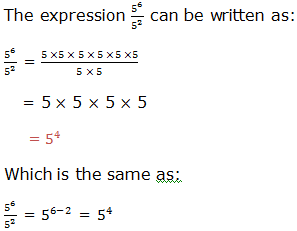
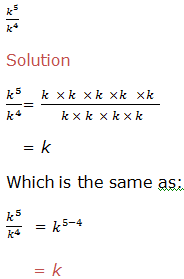
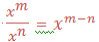
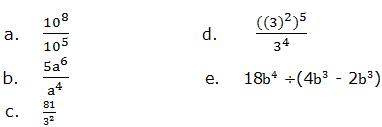
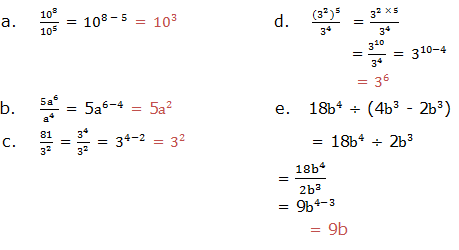
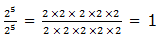
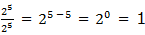
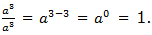
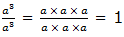


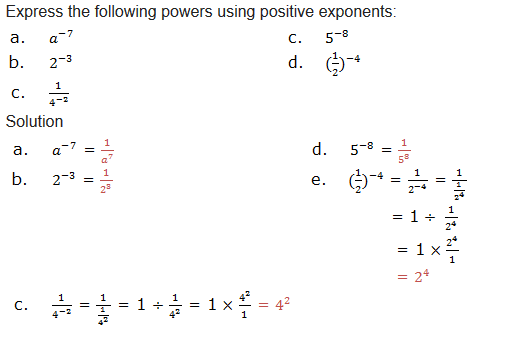



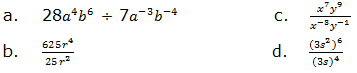
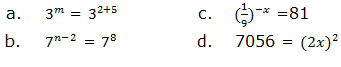
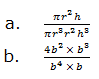


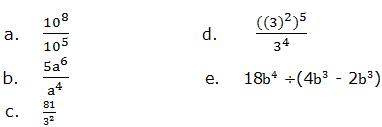
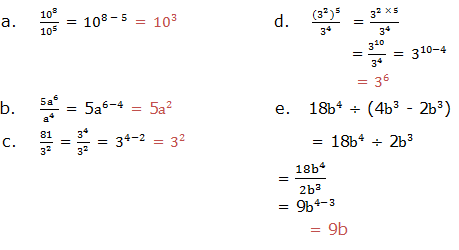
Exponents
Exponents tell how many times to use a number itself in multiplication. There are different laws that guides in calculations involving exponents. In this chapter we are going to see how these laws are used.
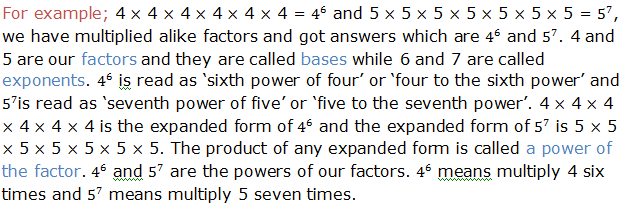
Single exponent tutorial
Tutorial Created by Willbald Mvungi-Ilboru Secondary
Indication of power, base and exponent is done as follows:

Solution:

To write the expanded form of the following powers:
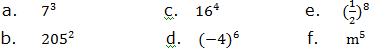
Solution
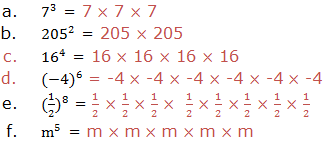
To write each of the following in power form:
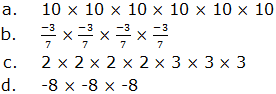
Soln.
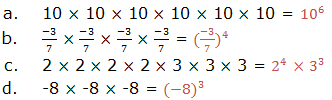
The Laws of Exponents
List the laws of exponents
First law:Multiplication of positive integral exponent
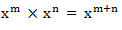
Second law: Division of positive integral exponent
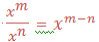
Third law: Zero exponents
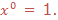
Fourth law: Negative integral exponents
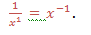
Verification of the Laws of Exponents
Verify the laws of exponents
First law: Multiplication of positive integral exponent
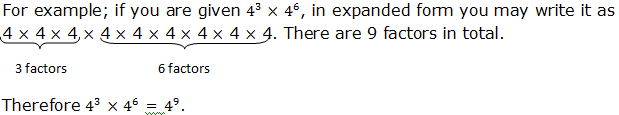
Exponent Multiplication Tutorial
Tutorial Created by Willbald Mvungi-Ilboru Secondary
Generally, when we multiply powers having the same base, we add their exponents. If x is any base and m and n are the exponents, therefore:
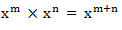
Example 1
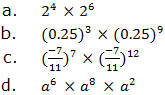
Solution
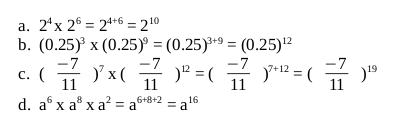
If you are to write the expression using the single exponent, for example,(63)4.The expression can be written in expanded form as:
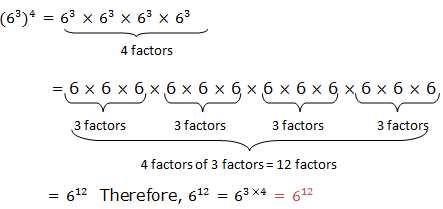
Generally if x is any real number, n and m are integers,
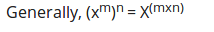
Example 2
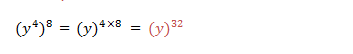
Example 3
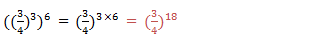
Example 4
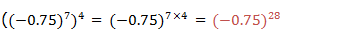
More examples below
Example 5
Rewrite the following expressions under a single exponent for those with identical exponents:
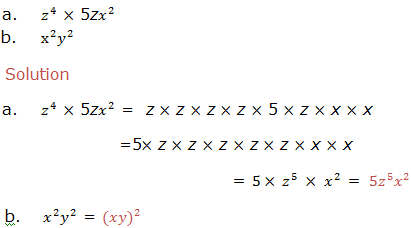
Second law: Division of positive integral exponent
Example 6
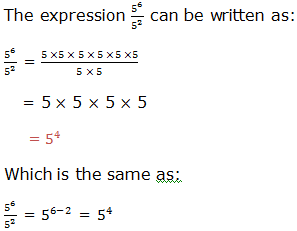
Example 7
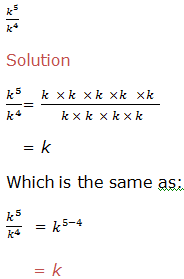
Therefore, to divide powers of the same base we subtract their exponents (subtract the exponent of the divisor from the exponent of the dividend). That is,
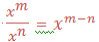
where x is a real number and x ≠ 0, m and n are integers. m is the exponent of the dividend and n is the exponent of the divisor.
Example 8
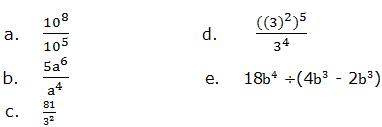
solution
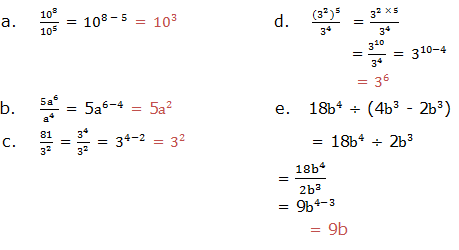
Third law: Zero exponents
Example 9
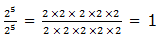
This is the same as:
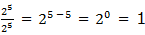
If a ≠ 0, then
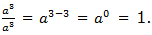
Which is the same as:
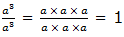
Therefore if x is any real number not equal to zero, then X0 = 1,Note that 00is undefined (not defined).
Fourth law: Negative integral exponents

Also;

Example 10
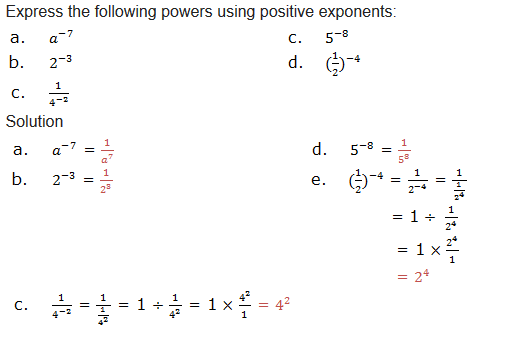
Exercise 1
1. Indicate base and exponent in each of the following expressions:

2. Write each of the following expressions in expanded form:

3. Write in power form each of the following numbers by choosing the smallest base:
- 169
- 81
- 10,000
- 625
a. 169 b. 81c. 10 000 d. 625
4. Write each of the following expressions using a single exponent:

5. Simplify the following expressions:
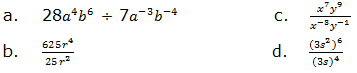
6. Solve the following equations:
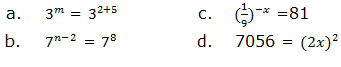
7. Express 64 as a power with:
- Base 4
- Base 8
- Base 2
Base 4 Base 8 Base 2
8. Simplify the following expressions and give your answers in either zero or negative integral exponents.
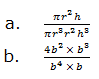
9. Give the product in each of the following:

10. Write the reciprocal of the following numbers:

Laws of Exponents in Computations
Apply laws of exponents in computations
Example 11
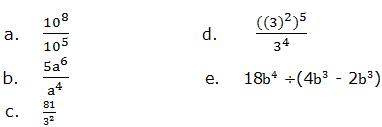
Solution
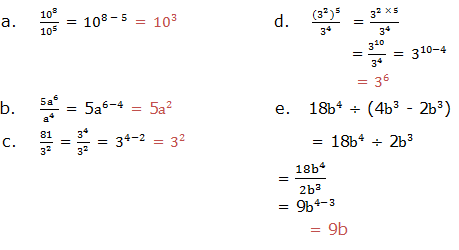
Radicals
Radicals
Simplify radicals
Radicals are opposite of exponents. For example when we raise 2 by 2 we get 4 but taking square root of 4 we get 2. The same way we can raise the number using any number is the same way we can have the root of that number. For example, square root, Cube root, fourth root, fifth roots and so on. We can simplify radicals if the number has factor with root, but if the number has factors with no root then it is in its simplest form. In this chapter we are going to learn how to find the roots of the numbers and how to simplify radicals.
When a number is expressed as a product of equal factors, each of the factors is called the root of that number. For example,25 = 5× 5;so, 5 is a square root of 25: 64 = 8× 8; 8 is a square root of 64: 216 = 6 ×6 ×6, 6 is a cube root of 216: 81 = 3 × 3 ×3 ×3,3 is a fourth root of 81: 1024 = 4 ×4 ×4 ×4 ×4, 4 is a fifth root of 1024.
Therefore, the nth root of a number is one of the n equal factors of that number. The symbol for nth root isn√ where√is called a radical and n is the index (indicates the root you have to find). If the index is 2, the symbol represents square root of a number and it is simply written as√without the index 2.n√pis expressed in power form as,
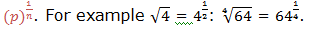
nth root of a number by prime factorization
Example 1, simplify the following radicals

Soution

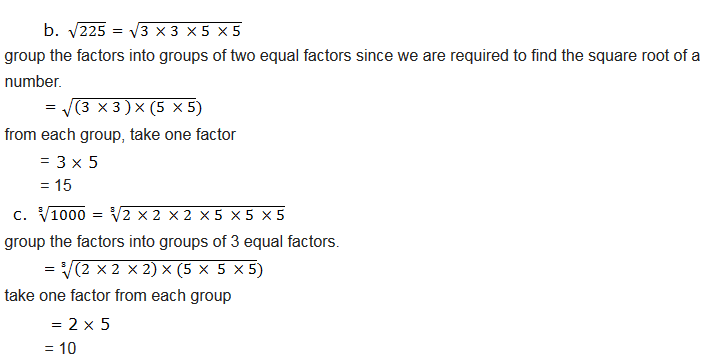
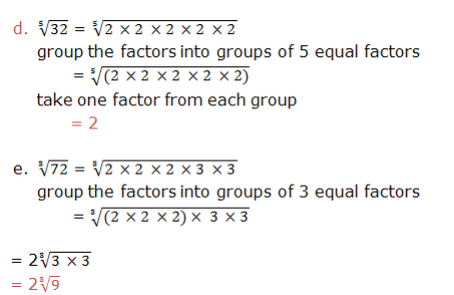
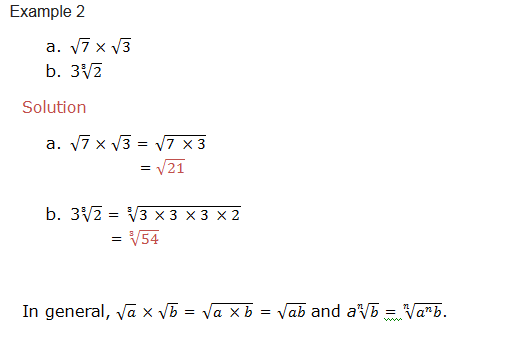
Basic Operations on Radicals
Perform basic operations on radicals
Different operations like addition, multiplication and division can be done on alike radicals as is done with algebraic terms.
Simplify the following:
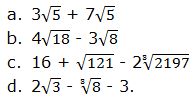
Solution
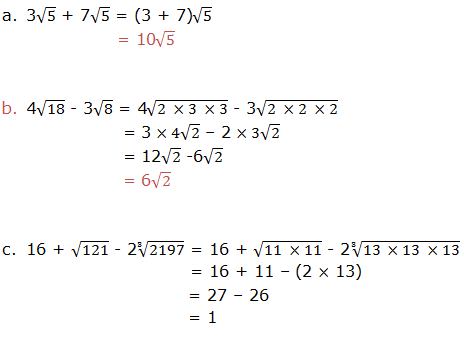
Simplify each of the following expressions:
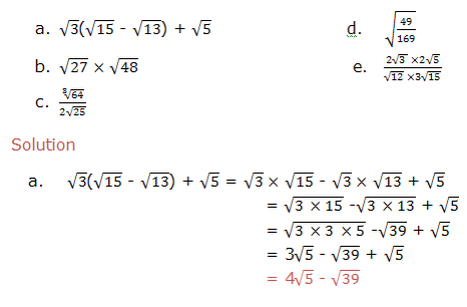
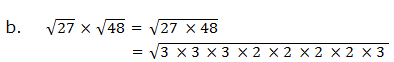
group the factors into groups of two equal factors and from each group take one of the factors.
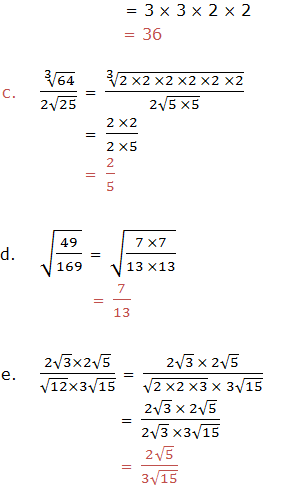
The Denominator
Rationalize the denominator
If you are given a fraction expression with radical value in the denominator and then you express the expression given in such a way that there are no radical values in the denominator, the process is called rationalization of the denominator.
Example 12
Rationalize the denominator of the following expressions:

Example 13
Rationalize the denominator for each of the following expressions:

Solution
To rationalize these fractions, we have to multiply by the fraction that is equals to 1. The factor should be considered by referring the difference of two squares.

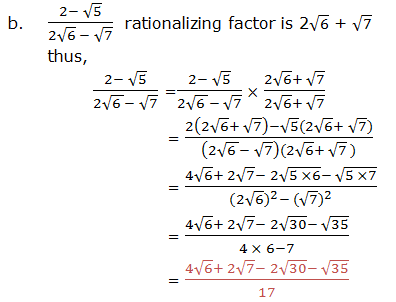


Exercise 2
1. Simplify each of the following by making the number inside the radical sign as small as possible:


Square Roots and Cube Roots of Numbers from Mathematical Tables
Read square roots and cube roots of numbers from mathematical tables
If you are to find a square root of a number by using Mathematical table, first estimate the square root by grouping method. We group a given number into groups of two numbers from right. For example; to find a square root of 196 from the table, first we have to group the digits in twos from right i.e. 1 96. Then estimate the square root of the number in a group on the extreme left. In our example it is 1. The square root of 1 is 1. Because we have two groups, this means that the answer has two digits before the decimal point. Our number is 196, read 1.9 in the table on the extreme left. From our number, we are remaining with 6, now look at the column labeled 6. Read the number where the row of 1.9 meet the column labeled 6. It meets at 1.400. Therefore the square root of 196 = 14.00 since we said that the answer must have2 digits before decimal points. Note: If you are given a number with digits more than 4 digits. First, round off the number to four significant figures and then group the digits in twos from right. For example; the number 75678 has five digits. When we round it off into 4 digits we get 75680 and then grouping into two digits we get 7 56 80. This shows that our answer has 3 digits. We start by estimating the square root of the number to the extreme left, which is 7, the square root of 7 is between 2 and 3. Using the table, along the row 7.5, look at the column labeled 6. Read the answer where the row 7.5 meets the column 6. Then go to where it is written mean difference and look at the column labeled 8, read the answer where it meets the row 7.5. Take the first answer you got where the row 7.5 met the column 6 and add with the second answer you got where the row 7.5 met the column 8 (mean difference column). The answer you get is the square root of 75680. Which is 275.1
Transposition of Formula
Re-arranging Letters so that One Letter is the Subject of the Formula
Re-arrange letters so that one letter is the subject of the formula
A formula is a rule which is used to calculate one quantity when other quantities are given. Examples of formulas are:

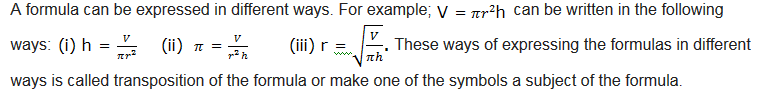
Example 14
From the following formulas, make the indicated symbol a subject of the formula:

Solution

Transposing a Formulae with Square Roots and Square
Transpose a formulae with square roots and square
Make the indicated symbol a subject of the formula:
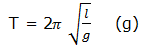
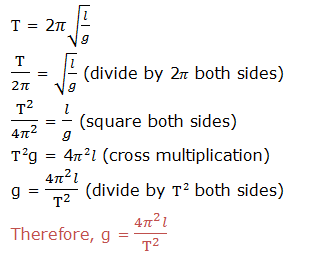
Exercise 3
1. Change the following formulas by making the given letter as the subject of the formula.

2. Use mathematical tables to find square root of each of the following:







Well and comfortable study
ReplyDeleteWow it's so enjoyable
ReplyDelete