Join Our Groups
TOPIC 6: CIRCLES
Definition of Terms
Circle, Chord, Radius, Diameter, Circumference, Arc, Sector, Centre and Segment of a Circle
Define circle, chord, radius, diameter, circumference, arc, sector, centre and segment of a circle
A circle: is the locus or the set of all points equidistant from a fixed point called the center.
Arc: a curved line that is part of the circumference of a circle
Chord: a line segment within a circle that touches 2 points on the circle.
Circumference: The distance around the circle
Diameter: The longest distance from one end of a circle to the other.
Origin: The center of the circle
Pi(π): A number, 3.141592..., equal to (the circumference) / (the diameter) of any circle.
Radius: Distance from center of circle to any point on it.
Sector: is like a slice of pie (a circle wedge).
Tangent of circle: a line perpendicular to the radius that touches ONLY one point on the circle. It always forms a right angle with the circle's radius.
NB: Diameter = 2 x radius of circle
Circumference of Circle = PI x diameter = 2 PI x radius
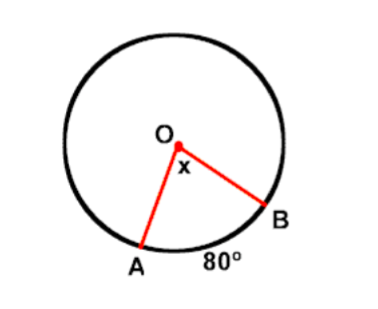
Central Angle
The Formula for the Length of an Arc
Derive the formula for the length of an arc
Circumference of a Circle = PI x diameter = 2 PI x radius where by PI =𝝅= 3.141592...
The Central Angle
Calculate the central angle
A central angle is an angle formed by two intersecting radii such that its vertex is at the center of the circle.
<AOB is a central angle. Its intercepted arc is the minor arc from A to B.

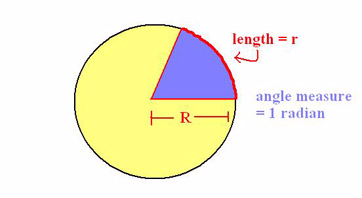
The Concept of Radian Measure
Explain the concept of radian measure
Radians are the standard mathematical way to measure angles. One radian is equal to the angle created by taking the radius of a circle and stretching it along the edge of the circle.
The radian is a pure mathematical measurement and therefore is preferred by mathematicians over degree measures. For use in everyday work, the degree is easier to work with, but for purely mathematical pursuits, the radian gives better results. You probably will never see radian measures used in construction or surveying, but it is a common unit in mathematics and physics.
Radians to Degree and Vice Versa
Convert radians to degree and vice versa
The unit used to describe the measurement of an angle that is most familiar is the degree. To convert radians to degrees or degrees to radians, the following relationship can be used.
angle in degrees = angle in radians * (180/pi)
So, 180 degrees = pi radians
Example 1
Convert 45 degrees to radians
Solution
45 = 57.32*radians
radians = 45/57.32
radians = 0.785
Most often when writing degree measure in radians, pi is not calculated in, so for this problem, the more accurate answer would be radians = 45 pi/180 = pi/4.
Example 2
Convert pi/3 radians to degree
degrees = (pi/3) * (180/pi)
degrees = 180/3 = 60°
Exercise 1
1. Change the following degree into radians:(a) 360 (b) 450 (c) 1350
2. Change the following radians into degrees: (a) 1 (b) 0.4 (c) 10
3. Find the degree for each of the following radians:(a) ∏/4 (b) 5∏ (c) 3∏/2
Angles Properties
Circle Theorems of Inscribed Angles
Prove circle theorems of inscribed angles
Inscribed Angle: an angle made from points sitting on the circle's circumference. Inscribed angle is formed when two secant lines intersect on a circle. It can also be formed using a secant line and a tangent line intersecting on a circle. A central angle, on the other hand, is an angle whose vertex is the center of the circle and whose sides pass through a pair of points on the circle, therefore subtending an arc. In this post, we explore the relationship between inscribed angles and central angles having the same subtended arc. The angle of the subtended arc is the same as the measure of the central angle (by definition).
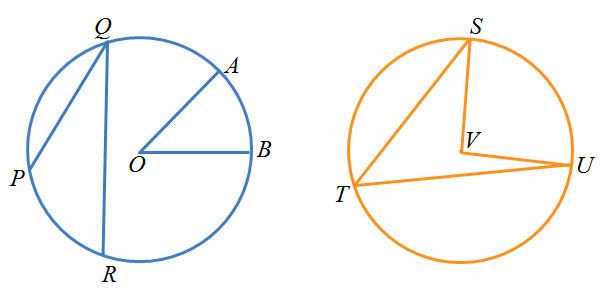
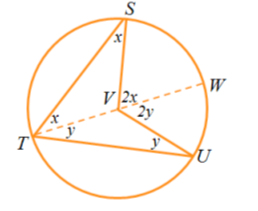
In the first circle, angle AOB is a central angle subtended by arc. Angle PQR is an inscribed angle subtended by an arc. In the second circle, angle STU is an inscribed angle and SVU is a central angle. Both angles are subtending by an arc.
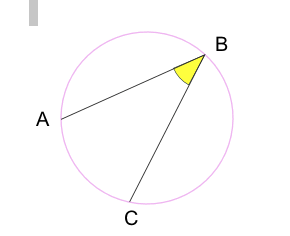
A and C are "end points" B is the "apex point"
What can you say about the two angles subtending the same arc? Draw several cases of central angles and inscribed angles subtending the same arc and measure them. Use a dynamic geometry software if necessary. Are your observations the same?In the discussion below, we prove one of the three cases of the relationship between a central angle and an inscribed angle subtending the same arc.
Theorem
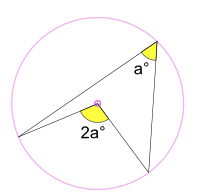
The measure of an angle inscribed in a circle is half the measure of the arc it intercepts. Note that this is equivalent to the measure of the inscribed angle and is half the measure of the central angle if they intercept the same arc. In a triangle STV, if we let the measure of angle STV be x, then angle TSV is also x, then angle SVW is 2x. This is also similar to triangle UTV. If we let angle UTV be y ,angle TUV also y, it follows that UVW is equal to 2y. In effect, the measure of the inscribed angle is half the central angle if sharing the same arc. (The angle which an arc subtends at the centre is double that which it subtends at any point on the remaining part of the circumference).
An inscribed angle a° is half of the central angle 2ao
Example 3
What is the size of Angle POQ? (O is circle's center)
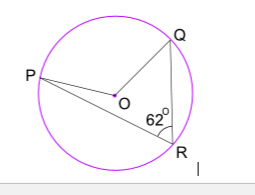
Angle POQ = 2 × Angle PRQ = 2 × 62° = 124°
Example 4
An arc subtends an angle of 20o at the center of the circle of radius25 cm. Find the length of this arc.
Exercise 2
1. Ac is a diameter of a circle ABCD. If BDC = 25o, Find angle ACB.
Theorem:
Angles inscribed by the same arc are equal.
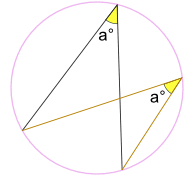
Example 5
What is the size of Angle CBX?
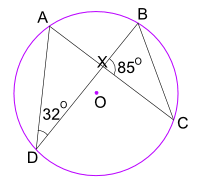
Angle ADB = 32° also equals Angle ACB. And Angle ACB also equals Angle XCB. So in triangle BXC we know Angle BXC = 85°, and Angle XCB = 32°, Now use angles of a triangle add to 180° : Angle CBX + Angle BXC + Angle XCB = 180°. Therefore, Angle CBX + 85° + 32° = 180° Angle CBX = 63°
Angle in a Semicircle:An angle inscribed in a semicircle is always a right angle: Proof of Theorem
Tangent Properties
A Tangent to a Circle
Describe a tangent to a circle
Tangent is a line which touches a circle. The point where the line touches the circle is called the point of contact. A tangent is perpendicular to the radius at the point of contact.
Tangent Properties of a Circle
Identify tangent properties of a circle
A tangent to a circle is perpendicular to the radius at the point of tangency. A common tangent is a line that is a tangent to each of two circles. A common external tangent does not intersect the segment that joins the centers of the circles. A common internal tangent intersects the segment that joins the centers of the circles.
Tangent Theorems
Prove tangent theorems
Theorem 1
If two chords intersect in a circle, the product of the lengths of the segments of one chord equal the product of the segments of the other.
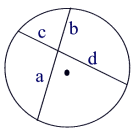
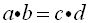
Intersecting Chords Rule: (segment piece)×(segment piece) =(segment piece)×(segment piece)
Theorem Proof:
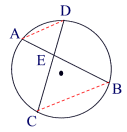
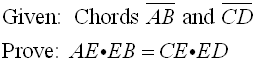
Exercise 3
1. Two chords AB and CD of a circle with centre o are produced to meet at P. AB =10 cm, CD = 6 cm, AO = 7 cm and APD = 90o . Calculate OP.
2. The radii of two concentric circles are 17 cm and 10 cm. A straight line ABCD cuts one circle at A and D and the other circle at B and C. If BC = 12 cm, calculate AB.
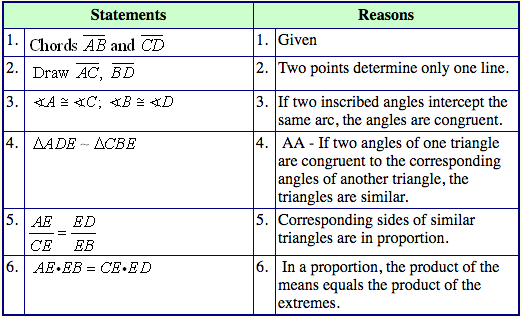
Theorem 2:
If two secant segments are drawn to a circle from the same external point, the product of the length of one secant segment and its external part is equal to the product of the length of the other secant segment and its external part.
Secant-Secant Rule: (whole secant)×(external part) =(whole secant)×(external part)
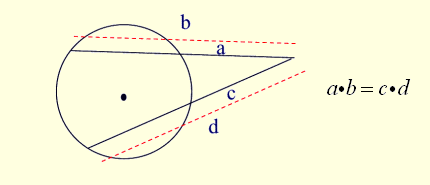
Theorem 3:
If a secant segment and tangent segment are drawn to a circle from the same external point, the product of the length of the secant segment and its external part equals the square of the length of the tangent segment.
Secant-Tangent Rule:(whole secant)×(external part) =(tangent)2
Theorems Relating to Tangent to a Circle in Solving Problems
Apply theorems relating to tangent to a circle in solving problems
Example 6
Two common tangents to a circle form a minor arc with a central angle of 140 degrees. Find the angle formed between the tangents.
Solution
Two tangents and two radii form a figure with 360°. If y is the angle formed between the tangents then y + 2(90) + 140° = 360°
y = 40°.
The angle formed between tangents is 40 degrees.
Exercise 4
1. The chords AB and CD of a circle meet at point O inside a circle. Given that AO = 8 cm, OC=7 cm and OD = 4 cm, find OB.
2. A chord XY of a circle of radius 6.8 cm subtends an angle of 420 at the centre of the circle. Find the difference in length between the chord XY and the minor arc XY.
Exercise 5
1. The tangent to a circle of radius 4.5 cm from an external point T is 6 cm long. Find the distance from T to the nearest point on the circumference.
2. The chords AB and CD of a circle meet at point O outside a circle. Given that AB = 4cm, CD = 4cm and OD = 2 cm, find OB.







Well ican understand but notes are very shalow
ReplyDelete