Join Our Groups
TOPIC 5: SEQUENCE AND SERIES






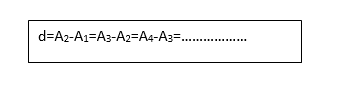


Geometric Progression (G.P).
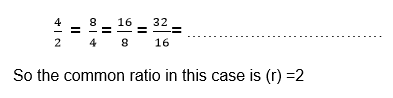

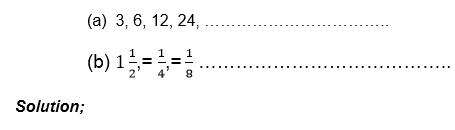



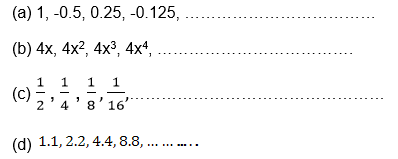

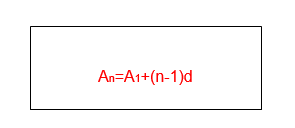


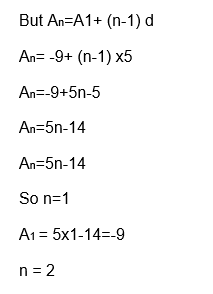




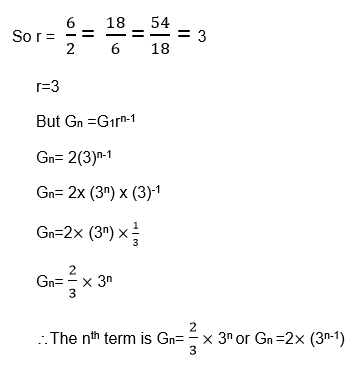
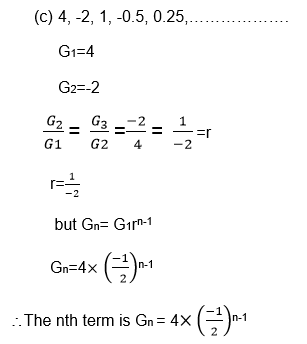
Sequences
The Concept of Sequence
Explain the concept of sequence
A Sequence is the arrangement of numbers or is a list of numbers following a clear pattern such that one number and the next are separated by comma (,).
Example: a1, a2, a3, a4 ……………………..
NB: Each number found in a Series or Sequence is called a term.
Example 1
Find the next three terms in the following sequences.
- 5, 8, 11, 14, 17,………………………………
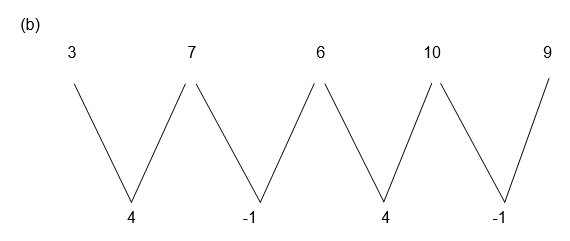
- 3, 7, 6, 10, 9, …………………………………
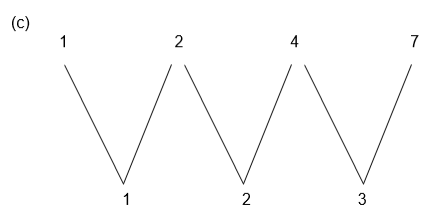
- 1, 2, 4, 7, ………………………………………
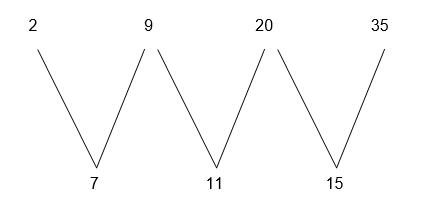
- 2, 9, 20, 35, …………………………………
Solution:
(a)You can see that each term is less to the next by 3.
So next three terms are (17+3),(17+3+3) and 17+3+3x3)
Which are 20, 23, and 26

Alternately add 4 and subs tract 1. The sequence then extends to 13, 12, 16

We see that the difference is increasing by 1 each time. So the next three terms are 11, 16 and 22.

The differences are increased by 4 each time, so the next three terms are 54, 77 and 104.
Example 2
Write down the first three terms in the sequences where the nth term is given by the formulae.

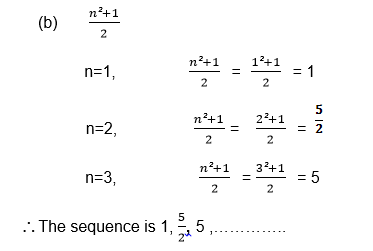

Example 3
The kth term of a series is k2 + 4
Find the sum of the first four terms in the series
Solution:
k=1, k2+4=12+4=5
k=2, k2+4=22+4=8
k=3, k2+4=32+4=13
k = 4, k2+4 = 42+4 = 20
So the series is 5+8+13+20 and its sum is 46
Example 4
Find the nth term of the following sequences:


Exercise 1
1. Write down the next three terms in the following sequences.

2. Find the first three terms in the sequence:
- 5n+2
- 1-3k
- n2+n+1
- 2n
3. Find the sum of the first four terms of the series where the kth term is given by:
- 5k+3
- k3-1
- 2k
4. Find the nth term of these sequences:

An Arithmetic Progression (AP) and Geometric Progression (GP)
Identify an arithmetic progression (AP) and geometric progression (GP)
When the series or sequence is such that between two consecutive terms there is a difference which is fixed, then the series or sequence is called an arithmetic progression (A.P)
The fixed difference (number) between two consecutive terms is called the common difference (d)
Example 5
In the sequence 4, 7, 19, 13, 16 there is a common difference which is
7-4=10-7=13-10=16-13=3.
So the common difference (d)=3.
Note that in arithmetic progression (A.P) the difference between two successive terms is always the same.
Sometimes numbers may be decreasing instead of increasing, the arithmetic sequence or series while terms decrease have a negative number as a common difference.
Example 6
The common difference of the sequence 6, 4, 2, 0, -2, …………………… is?
In general if A1, A2, A3, A4, ……………………… An are the terms of the arithmetic sequence , then the common difference is ;
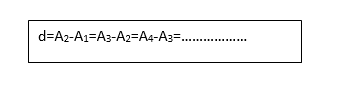
Example 7
For each of the following sequences, find the common difference and write the next two terms.

Solution:

Exercise 2
1. Find the common difference for each of the following sequence:
- 11, 14, 17, 20, …………………………………
- 2, 4, 6, 8, 10, ……………………………………
- 0.1, 0.11, 0.111, 0.1111 , …… … … … … …
- y, y+3, y+6, y+9, y+12, … …… … … … ……
2. State whetherthe following sequence are arithmetic or not:
- 2, 5, 8, 11, 14, …………… ……………… ……
- 1, 3, 4, 6, 7, 9, 10, ………………………………
- y, y + x, y+2x, y+3x, … ………… ……
3. The temperatureat a mid day is 30c, and it falls by 20c each hour. Find the temperature at the end of the next four hours.
Geometric Progression (G.P).
When the series or Sequence is such that between two consecutive terms there is a ration which is fixed, then the series or sequence is called a geometric progression (G.P)
The fixed ratio(number) between two successive terms is called the common ratio (r).
Example 8
In 2, 4, 8, 16, 32, … … …… … … …….
There is a common ration which is
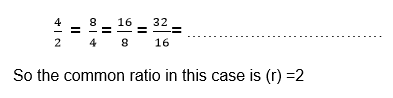
Note that like in arithmetic progression (A.P), in geometric progression (G.P) the common ratio does not change.
Also the terms may be decreasing instead of increasing, the geometric sequence or series whose terms decrease have a positive common ratio which is less than 1 for the progression with positive terms.

Example 9
For each of the following sequence find the common ratio.

Example 10
For the following geometric sequences, find the common ratio and write down the next two terms:

The next term is found by multiplying the term considered to be the last term by the common ratio.

Exercise 3
1. Which of the following sequences are geometric
- 1, 2, 4, 8, 16, ……………………………………
- 2, 6, 18, 54, 162, …………………………………
- 1, -1,1,-1,1, ………………………………………
- x2, 2x3, 4x4, 8x3…………………………………
- 1, 2, 4, 7, 10, ………………………………………
- 0.1, 0.2, 0.3, 0.4, 0.5, ……………………………
- 3, 6, 9, 12,15, ……………………………………….
2. Find thecommon difference for each of the following geometric progressions (G.P)
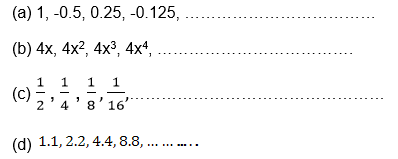
3. Find thenext term of the sequence 2, 10, 50, 500,………………….
4. The populationof a town is decreasing so that every year the population declines by a quarter. If the population is originally 100,000. What will it be after 5 years?
The General Term of an AP
Find the general term of an AP
If A1, A2, A3, …………………An are the terms of an arithmetic sequence, then there is a common difference d which is given by
d = A2 – A1 = A3 – A2 = An – An – 1

But . A3 = A1 + 2d which means
A4 =[ A1+2d]+d
= A1 + 3d
Putting into consideration this pattern, it is true that
A5 = A1 + 4d
A6 = A1 + 5d
An = A1 + (n-1)d
Where An is the nth term
The nth term of the sequence with first term A1 and common difference d is given by
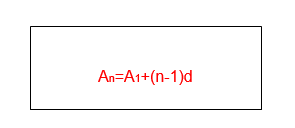
Example 11
Find theformula for the nth term of the sequence 8 , 9.5, 11, 12.5, 14, 15.5,……

Note that the nth term gives every term in the sequence,
For example when n=3, you have A3=1.5x3+6.5=11
So A3=11 where 11 is given in the sequence above having the third position.
Therefore An shows the position of the term in sequence and of A1+(n-1)d gives the value of the term for any positive integer.
Example 12
The 5th term of an arithmetic sequence is 11, and the 8th term is 26. Find the first five terms.

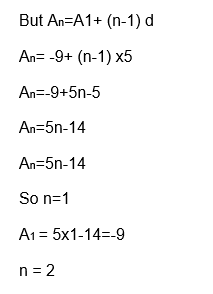

Example 13
The 8th term of an arithmetic sequence is 9 greater than the 5th term, and the 10th term is 10 times the 2nd term. Find
- The common difference (d)
- 20th term.


Example 14
Find the formula for the nth term of each of of the following geometric sequence.
- 2, 6, 18, 54 , ………………………………
- 4,-2, 1, -0.5, 0.25 …………………………

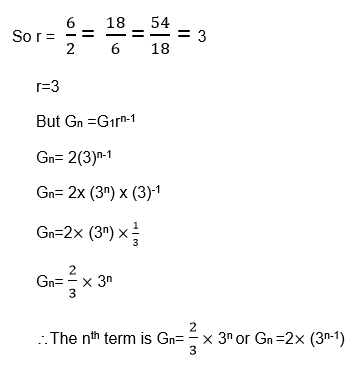
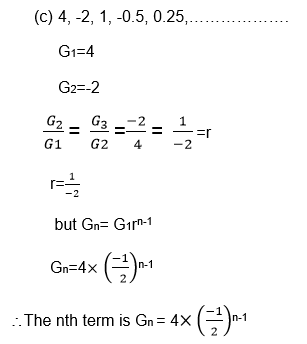
Series
The Formula for a Sum of an Arithmetic Progression
Derive the formula for a sum of an arithmetic progression
When the terms are separated by addition (+) sign, there we have what we call a series.
Example: 2+4+6+8+……………………………
Is a series with the first term (A1) 2 and common difference (d) 2
It is possible to establish a formula for the sum of the first n terms of the arithmetic progression.
Let Sn denote the sum of the first n terms of the arithmetic series.
Consider the sum of the first 5, terms of arithmetic progression (AP) whose first term is 1 and whose common difference (d) is 1.
So S5 = A1+A2+A3+A4+A5
S5=1+2+3+4+5 ………………………….. (1)
The first case is the sum of five terms which are increasing from 1 up to 5 while the second case shows the same sum but the terms are decreasing from 5 to 1.
If you add (1) and (2) together, you find that
S5+S5=(1+5) + (2+4) +(3+3) + (4+2) + (5+1)
25s = 6+6+6+6+6
255=30
Dividing by 2 each side gives

Also we can write

Example 15
Find the sum of the first 20 terms of the series.

Example 16
Find the sum of the series 4+7+10+13+…………….+304
Solution:
To use the formula for summation of n terms, you must know how many terms are there, i.e finding the value of n;
Now
A1=4, d=3 and An = 304 n=?
An =A1+ (n-1)d
304 = 4+ (n-1)x3
304 = 4+3n-3
304=3n+1
304=3n

Example 17
How many terms of the series 1+3+5+7+………………. are needed to make the sum of 169?

Exercise 4
1. Find thesum of the first 20 terms of the series
- 2+5+8+11+……………………
- 19+16+13+10+7+……………
2. Find thenumber of terms and the sum of the series:
- 1+3+5+7+ ……………………………………
- 40+37+34+31+…………………+-257
3. The sumof the first 10 terms of an arithmetic progression (A.P) is 40, and the sum of the next 10 terms is 80. Find the sum of the first five terms of the series.
4. One dayFrola spends 40 minutes of her home work. The length of time she spends increase by 4 minutes each day. Find the total length of time she spends after eight days.
The Arithmetic Mean
Calculate the arithmetic mean
Remember that the arithmetic mean (M) of n numbers is found by adding them and then dividing the sum by n, e.g the arithmetic mean of a,b,c and d is
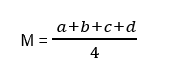
The Formula for the Sum of a Geometric Progression
Derive the formula for the sum of a geometric progression
Geometric series are the series that can be written as
G1+G2+G3+ ………………………..Gn
Example: 2+4+8+16+ ………………………..+Gn
Or 1+3+9+27+81+…………………….
Suppose we want to find the sum of 1+3+9+9+27+81+…………………
S5=!+3+9+27+81……………………….(1)
If we multiply sn by the common ratio(r), we have.
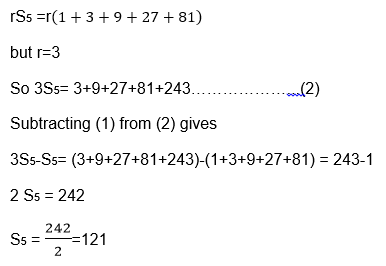

Example 18
1. Find the sum of the geometric series 2+4+8+ ………………..+2048
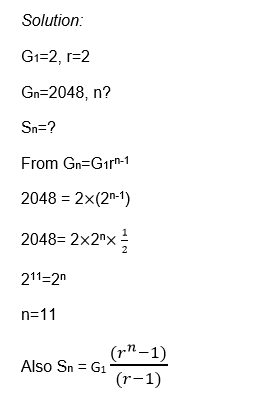
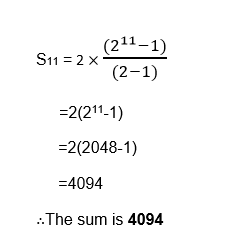
Example 19
Find the sum of the first 8 terms of the series 5+20+80+320+ ……………
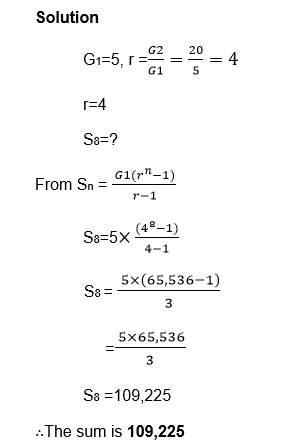
Exercise 5
1. For each ofthe following series, find the number of terms and hence the sum of the series.
- 1+3+9+…………………+729
- 1-2+4-8+………………+1,024

The Geometric Mean
Calculate the geometric mean
The Geometric mean (GM) of n positive numbers is found by taking the nth root of their product.
Example 20
The Geometric mean of a, b, c and d is
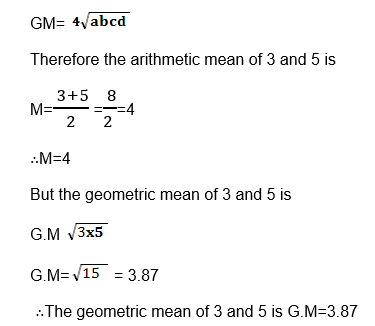
The arithmetic mean and geometric mean can be used to check that a sequence is an arithmetic or geometric respectively.
FACTS:
- If a, b and c are consecutive three term of arithmetic progression (A.P), then b is the arithmetic mean of a and c
- If a, b and c are three consecutive terms of geometric progression (G.P), then b is the geometric mean (G.M) of a and c.
Proof:


Example 21
Find the arithmetic and geometric means of

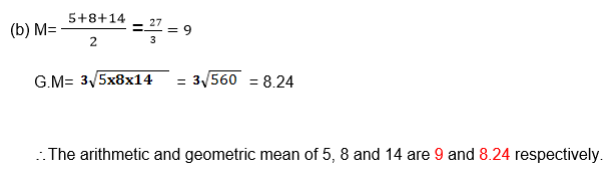
Exercise 6
1. Find the arithmetic and geometric means of the following;
- x1, x3
- 4x, 9x
- 4a, 25a.
2. The arithmeticmean and geometric mean of two numbers are 7.5 and 6 respectively. Find the two numbers.
Compound Interest
Compound Interest using Formula
Calculate compound interest using formula
Suppose money is invested or borrowed. At the end of a year, interest is calculated. Suppose this interest is added to the original principal, and at the end of the next year interest is added to the new principal. This process may be continued for a number of years.
This process is called COMPOUND INTEREST.
When money is invested at a compound interest, the amount of money increase as a geometric sequence.
Example 22
Ibrahimu invested 20,000/= at 6% compound interest. How much was there after 5 years?

Now let the principal be P, the rate R% and the time in years be n.

Example 23
At the beginning of each year Martha invests 10,000/= at 5% compound interest. How much does she have at the end of the 10th year?
Solution:
She has made 10 different investments each giving different amount of interest.
The 1st investment has had 10 years of interest, hence it is 10,000 x (1.05)10
The 2nd investment has had 9 years of interest. So it is 10,000 x (1.05)9
The 3rd investment has had 8 years of interest. Hence it is 10,000 x (1.05)8
Following this pattern,
The 10th investment has had 1 year of interest. Hence it is 10,000 x 1.05.
The sum of all these amounts is given by;
10,000x1.0510 +10,000 x1.059+ 10,000x1.058+……………+10,000x1.05
This geometric series with first term 10,000 x 1.05 and common ratio 1.05.
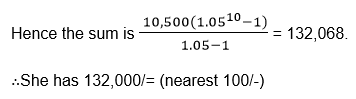
Exercise 7
1. Find thetotal amount of the following savings if they earn compound interest.
- 100,000/= for 2years at 6% p.a
- 250,000/= for 3 years at 4.5% p.a
- 400,000/= for 20years at 5.5% p.a
2. A populationis increasing at 2% if it starts at 10,000,000 what will it be after 20 years.
3. At the beginning of each year 600,000/= is invested at 6% compound interest.Find the total value of the investment at the end of the 15th year.







EmoticonEmoticon