MATHEMATICS: FORM THREE: Topic 7 - THE EARTH AS A SPHERE

 Join Our Groups

TELEGRAM | WHATSAPP

Schemes of Work 2024

Necta Timetables 2024

English Course - Free

Kenya Notes

TOPIC 7: THE EARTH AS A SPHERE

Features and Location of Places

The Equator, Great Circle, Small Circles, Meridian, Latitudes and Longitudes

Describe the equator, great circle, small circles, meridian, latitudes and longitudes

Definition of latitude and longitude

The Earth is not a perfect sphere, as it is slightly flatter at the north and south poles than at the equator. But for most purposes we assume that it is a sphere.

The position of any point on earth is located by circles round the earth, as follows:

The earth rotates about its axis, which stretches from the north to the South Pole.

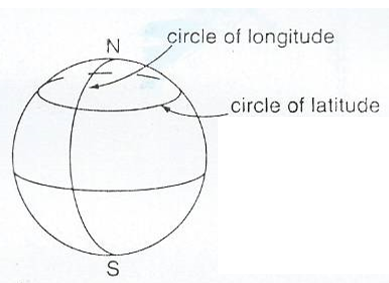
Circles round the Earth perpendicular to the axis are circles of Latitude and Circles round the Earth which go through the poles are circles of Longitude or meridians.

Consider the following diagram

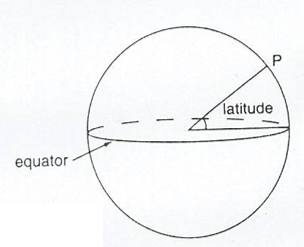
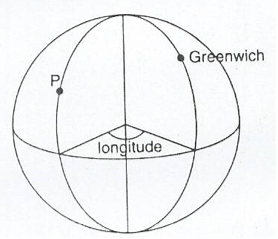
Normally Latitude is defined relative to the equator, which is the circle of latitude round the middle of the Earth while Longitude is defined relative to the circle of longitude which passes through Greenwich in London (Greenwich meridian).

The latitude of a position tells us how far north or south of the equator it is while the longitude of a position shows us how far east or west of the Greenwich meridian it is.

Latitude; If we draw a line from the centre of the Earth to any position P , then the angle between this line and the plane of the equator is the latitude of P.

Longitude: This is the angle between the plane through the circle of any Longitude P and the plane of the Greenwich meridian .

Latitude can be either North or South of the equator while Longitude can be either East or West of Greenwich.

When locating the latitude and longitude of a place we write the latitude first then longitude.

Example 1

Dar es Salaam has latitude 7°S (i.e. 7° south of the equator) and longitude 39°E (i.e. 39° east of the Greenwich meridian). So Dar es Salaam is at (7°S, 39°E).

NB; Greenwich itself has latitude 51°N ( i.e. 51° north of the equator)and longitude 0° (by definition). Johannesburg has latitude 26°S (i.e. 26 south of the equator) and longitude 28°E(i.e. 28°east of the Greenwich meridian), therefore Johannesburg is at (26°S, 28°E).The north pole has latitude 90°S but its longitude is not defined. ( Every circle of longitude goes through the north pole).The south pole has latitude 90°s. Its longitude is not defined. So all points on the equator (such as Nanyuki in Kenya) have latitude 0°

Ranges; Latitude varies between 90°S (at the south pole) to 90°N (at the north pole).

Ranges; Latitude varies between 90°S (at the south pole) to 90°N (at the north pole). Longitudevaries between 180°E and 180°W. These are the longitudes on the opposite side of the Earth from Greenwich.

GREAT AND SMALL CIRCLES: There is an essential difference between latitude and longitude. Circles of longitude all have equal circumference. Circles of latitude get smaller as they approach the poles. The centre of a circle of longitude is at the centre of the earth. They are called great circles. For circles of latitude, only the equator itself is a great circle. Circles of latitude are called small circles.

Example 2

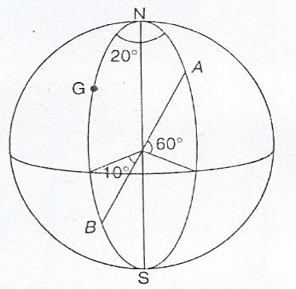
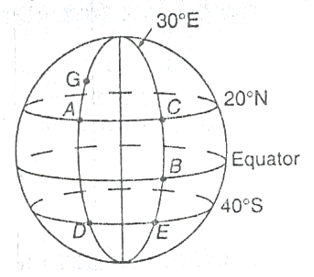
Find the latitudes and longitudes of A and B on the diagram below;

Solution;

The point A is 60° above equator, and 20° east of Greenwich.

So the point A is at (60°N, 20°E)

The point B is 10° below the equator, and on the Greenwich meridian.

So the point B is at (10°S, 0°).

Exercise 1

1. Write down the latitude and longitude of the places shown on figures below:

2. Copy the diagram show on the figure above and mark these points:

1. (10°N, 30°E)
2. (20°N, 20°W)
3. (0°, 20°W)

3. Obtain a globe, and on it identify the following places.

1. (40°S, 30°E)
2. (50°S,20°W)
3. (10°N,40°W)
4. (40°N, 30°E)
5. (80°N,10°E)
6. (0°,0°)

Difference between angles of latitude or longitude

Suppose two places have the same longitude but different latitudes. Then they are north and south of each other.

In finding the difference between the latitudes take account of whether they are on the same side of the equator or not.

• If both points are south of the equator subtract the latitudes
• If both points are the north of the equator subtract the latitudes
• If one point is south of the equator and the other north then add the latitudes

Similarly, suppose two places have the same latitudes but different longitudes:

• If both points are east of Greenwich subtract the Longitudes
• If both points are west of Greenwich subtract the Longitudes
• If one point is east of Greenwich and the other west then add the longitudes

Suppose places A and B are on the same longitude, then the difference in latitude is the anglesubtended by AB at the centre of the earth.

Suppose places A and B are on the same latitude.

Then the difference in longitude is the angle subtended by AB on the earth's axis.

Locating a Place on the Earth’s Surface

Locate a place on the Earth’s surface

Example 3

Three places on longitude 30°E are Alexandria (in Egypt) at (31°N, 30°E), Kigali (in Rwanda) at (2°S, 30°) and Pietermaritzburg (in South Africa) at (30°S, 30°E).

Find the difference in latitude between

1. Kigali and Pietermaritzburg
2. Kigali and Alexandria

Solution

(a)Both Towns are south of the equator. So subtract the latitudes. 30 – 2 = 28

Therefore the difference is 28⁰

(b) Kigali is south of the equator, and Alexandria is north, so add the latitudes

31 + 2 = 33

The difference is 33⁰

Example 4

A plane starts at Chileka airport (in Malawi) which is at (16°S, 35°E). It flies west for 50°. What is its new latitude and longitude?

Solution

Since it flies west, then subtract 35° from 50°. This gives 15°

The new longitude is now west of Greenwich, hence the plane is at (16°S, 15°W).

Exercise 2

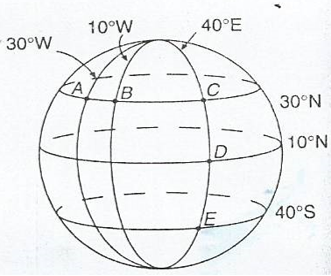
1. In the diagram shown in the following figure find,

1. The difference in longitude between A and B
2. The difference in longitude between D and E

Distances along Great Circles

Distances along Great Circles

Calculate distances along great circles

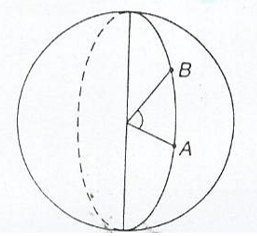
Take two places X and Y on the same line of longitude, i.e. one place is due north of the other. Suppose X is due north of Y. When travelling north from Y to X, you travel along part of a circle of longitude that is you travel along an arc of the circle.

The diagram below shows two points A and B on the same circle of longitude.

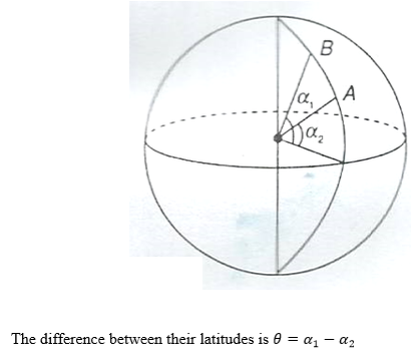
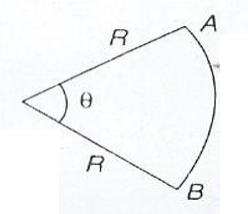
In the figure above, the sector containing the arc AB subtending∅, is shown.

Recall the formula for the length of arc.

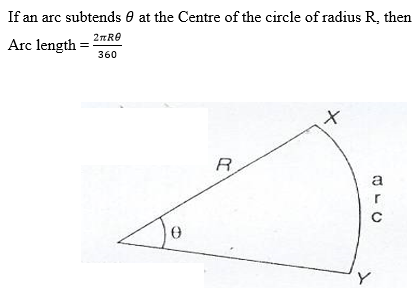
NB: Remember, to find the difference in latitudes, take account of whether the places are north or south of the equator. If they are all found in south or north, then subtract the latitudes. If one is south and the other North then add the latitudes.

Nautical miles

Navigation Related Problems

Solve navigation related problems

Example 5

Find the distance between Alexandria (31°N, 30°E) and Kigali (2°S, 30°E)

Solution

Example 6

A plane starts at (20⁰S, 30⁰E), and flies north for 4000 km. Find its new latitude and longitude.

Example 7

A plane flies north from (10°S, 30°E) to ((27°N, 30°E) taking a time of 3 hours.

Find its speed, giving your answer I both knots and kilometers per hour.

Exercise 3

Consider the following Questions.

Distances along Small Circles

Distance along Small Circles

Calculate distance along small circles

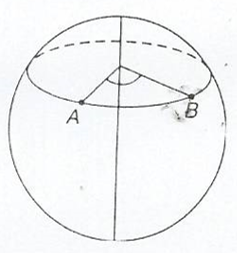
Suppose P and Q are places west or east of each other, i.e they lie on the same circle of latitude. Then when you travel due east or west from P to Q you travel along an arc of the circle of latitude.

The situation here is slightly different from that of the previous section. While circles of longitude all have the same length, circles of latitude get smaller as they get nearer the poles.

Consider the circle of latitude 50°S. Let its radius be r km.

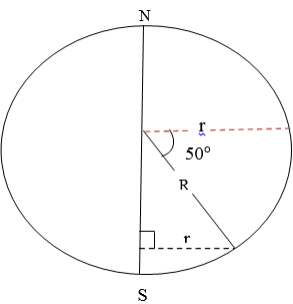
Nautical miles

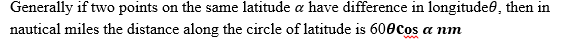
Example 8

Find the distance in km and nm along a circle of latitude between (20°N, 30°E) and (20°N, 40°W).

Solution:

Both places are on latitude 20°N. The difference in longitude is 70°. Use the formula for distance.

Distance = 111.7 cos20° x 70°. Hence the distance in nautical miles is 60 x 70 x cos20°

The distance is 3,950 nm.

Example 9

A ship starts at (40°S, 30°W) and sails due west for 1,000 km. Find its new latitude and longitude.

Example 10

A ship sails west from (20°S, 15°E) to (20°S, 23°E), taking 37 hours. Find speed, in knots and in kms per hr.

Exercise 4

Consider the following Questions.

Navigation

Suppose a ship is sailing in a sea current, or that a plane is flying in a wind. Then the course set the ship or plane is not the direction that it will move in. the actual direction and speed can be found either by scale or by the use of Pythagoras’s theorem and trigonometry.

Draw the line representing the motion of the ship relative to the water. At the end of this line draw a line representing the current. Draw the third side of the triangle. This side, shown with a double – headed arrow, is the actual course of ship.

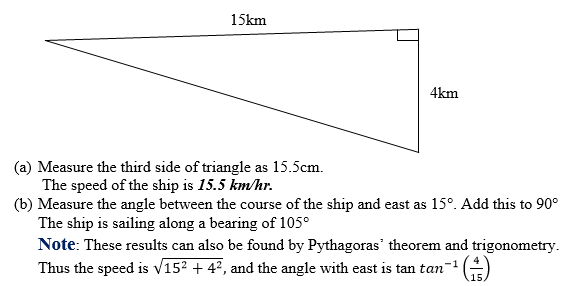
Example 11

A ship sets course due east. In still water the ship can sail at 15km/hr. There is a current following due south of 4kkm/hr. use a scale drawing to find.

1. The speed of the ship
2. The bearing of the sip.

Solution:

In one hour the ship sails 15km east relative to the water. Draw a horizontal line of length 15cm. In one hour the current pulls the ship 4km south. At the end of the horizontal line, draw a vertical line of length 4cm.

Example 12

The ship of example 10 needs to travel due east. Calculate the following.

1. What course should be set?
2. How long will the ship take to cover 120km?

Solution

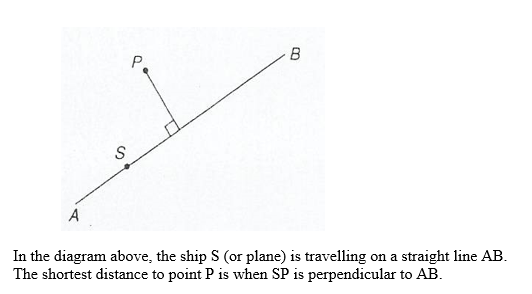
The ship needs to set a course slightly north of east, consider the following diagram.

Note: With no current, the journey would take 8hrs. The journey takes slightly longer when there is a current.Suppose a ship or a plane does not directly reach a position. We can still find how close the ship or plane is to the position.

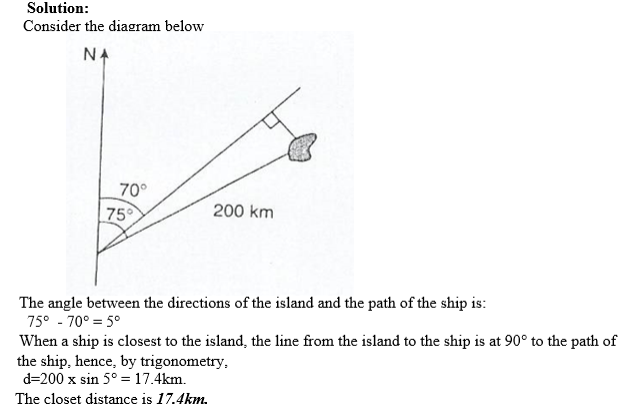
Example 13

A small island is 200km away on a bearing of 075°. A ship sails on a bearing of 070°.Find the closest that the ship is to the island.

Exercise 5

1. Find the difference in longitude between Cape Town (34°S, 18°E) and Buenos Aires (34°S, 58°W)

2. A ship startsat (15°N, 30°W) and sails south for 2,500km. Where does it end up?

3. Find thedistance in km along circle of latitude between cape Town and Buenos aires (see question 2)

4. A plane starts at (37°S, 23°W) and flies east for 1,500 km. where does it end up?

5. Find thedistance in nautical miles between the places in question 1.

6. A plane startsat (43°N, 17°E) and flies west for 960nm. Where does ie end up?

7. A sea current of6 km/hr flows due east. A ship that can sail at 19 km/hr in still water sets a course due south. Find the following by scale drawing.

1. The direction in which the ship sails
2. The actual speed of the ship

8. The ship of question 4 needs to travel due south. How long will the ship take to travel 260 km

9.A plane flies on a bearing of 342°.There is a control tower 100 km from the plane on a bearing of 350°. Find the shortest distance between the plane and the control tower.

10. A lighthouse is 150 km from ship on a bearing of 123°. The ship sails on a bearing of 138°. Calculate the shortest distance between the ship and the lighthouse