MATHEMATICS: FORM TWO: Topic 8 - PYTHAGORAS THEOREM

 Join Our Groups

TELEGRAM | WHATSAPP

Schemes of Work 2024

Necta Timetables 2024

English Course - Free

Kenya Notes

TOPIC 8: PYTHAGORAS THEOREM

Triangle with a Right angle i.e. 90° has an amazing property. Do you want to know what property is that? Go on, read our notes to see the amazing property of a right angled triangle.

Pythagoras Theorem deals only with problems involving any Triangle having one of its Angles with 90⁰. This kind of a Triangle is called Right angled triangle.

When triangle is a right angled triangle, squares can be made on each of the three sides. See illustration below:

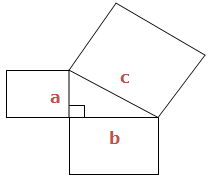
The Area of the biggest square is exact the same as the sum of the other two squares put together. This is what is called Pythagoras theorem and it is written as:

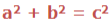
that is:

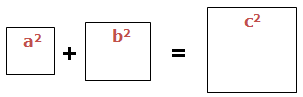
‘c’ is the Longest side of the Triangle, is called Hypogenous and is the one that forms the biggest square. aand b are the two smaller sides.

Proof of Pythagoras Theorem

The Pythagoras Theorem

Prove the pythagoras theorem

Pythagoras theorem states that: In a Right Angled Triangle, the sum of squares of smaller sides is exactly equal to the square of Hypotenuse side (large side). i.e. a² + b² = c²

Take a look on how to show that a² + b² = c²

See the figure below:

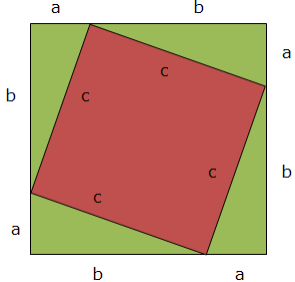
The area of a whole square (big square)

A big square is the one with sides a + b each. Its area will be:

(a + b) ×(a + b)

Area of the other pieces

First, area of a smaller square (tilted) = c²

Second, area of the equal triangles each with bases a and height b:

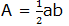
But there are 4 triangles and they are equal, so total area =

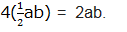
Both areas must be equal, the area of a big square must be equal to the area of a tilted square plus the area of 4 triangles

That is:

(a + b)(a + b) = c² + 2ab

Expand (a +b)(a + b): a² +2ab + b² = c² + 2ab

Subtract 2ab from both sides: a² + b² = c² Hence the result!

Note: We can use Pythagoras theorem to solve any problem that can be converted into right Angled Triangle.

Exercise 1

1. In a right triangle with given hypotenuse c and legs a and b, find:

1. c if a = 5 and b = 12
2. a if b = 8 and c = 12
3. b if a = 9 and c = 11

2. A rectangle has base 6 and height 10. What is the length of the diagonal?

3. A square has a diagonal with length 6. What is the length of the sides of the square?

4. The diagonals of a rhombus have lengths 6 and 8. Find the length of one side of the rhombus.

5. A ladder leans against a wall. If the ladder reaches 8m up the wall and its foot is 6m from the base of the wall. Find the length of the ladder.

6. Find the value of the marked side.

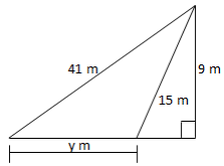
Application of Pythagoras Theorem

The Pythagoras Theorem to Solve Daily Life Problems

Apply the pythagoras theorem to solve daily life problems

You may have heard about Pythagoras's theorem (or the Pythagorean Theorem) in your math class, but what you may fail to realize is that Pythagoras's theorem is used often in real life situations. For example, calculating the distance of a road, television or smart phone screen size (usually measured diagonally).

Activity 1

Apply the pythagoras theorem to solve daily life problems