Join Our Groups
TOPIC 6: SIMILARITY
Some Figures tend to have different size but exactly equal angles and their corresponding sides always proportional. This kind of figures are said to be similar. Read the notes below to see which shapes are said to be similar.
Here is a well prepared tutorial on Similarity
Tutorial Created by Willbald Mvungi-Ilboru Secondary
Similar Figures
Two geometrical figures are called similar if they both have the same shape. More precisely one can be obtained from the other by uniformly scaling (enlarging or shrinking). Possibly with additional translation, rotation and reflection. Below are similar figures, the figures have equal angle measures and proportional length of the sides:
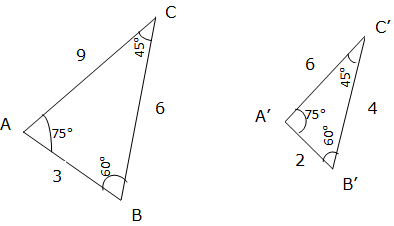
Angle A corresponds to angle A’, angle B corresponds to B’, angle C corresponds to C’ also each pair of these corresponding sides bears the same ratio, that is:
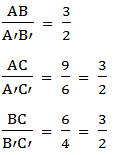
Since all sides have the same ratio i.e. they are proportional and the corresponding angles are equal i.e. angle A = angle A’, angle B = angle B’ and angle C = angle C’, then the two figures are similar. The symbol for similarity is '∼'
Note: all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand rectangles are not all similar to each other, isosceles triangles are not all similar to each other and ellipses are not all similar to each other.
Similar Polygons
Identify similar polygons
Two Triangles are similar if the only difference is size (and possibly the need to Turn or Flip one around). The Triangles below are similar

(Equal Angles have been marked with the same number of Arcs)
Similar Triangles have:
- All their angles equal
- Corresponding sides have the same ratio
For example; Given similar triangles below, find the length of sides a and b
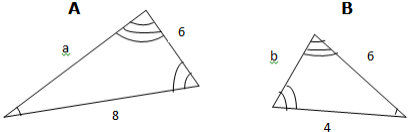
Solution
Since we know that, similar triangles have equal ratio of corresponding sides, finding the ratio of the given corresponding sides first thing:


How to find if Triangles are Similar
Two Triangles are similar if:
- All their equals are angles
- The corresponding sides are in the same ratio
But we don’t need to know all three angles and all three sides, even two or three are enough.
Intercept theorem
The theory is also called Side-Splitter theorem. Let ABC be any Triangle and DE is drawn parallel to BC, then AD/DB = AE/EC.
To show this is true draw a line DF parallel to EC
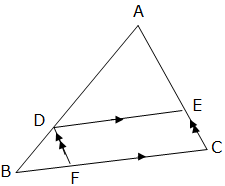
The Triangles ADE and BD have exactly equal angles and so they are similar (recall that the two Triangles are similar by AA).
Side AD corresponds to side DB and side AE corresponds to side DF, thus AD/DB = AE/DF But DF = EC, so AD/DB = AE/EC
Similarity Theorems of Triangles
Prove similarity theorems of triangles
There are three ways to find that the two Triangles are Similar
1. AA (Angle-Angle): this means, Triangles have two of their Angles equal. See an illustration below
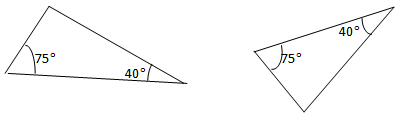
If two of their Angles are equal then the third Angle must also be equal, because Angles of a Triangle add up to1800. In our case, our third Angle will be:
1800 - (750 + 400) = 650
Therefore, AA can also be called AAA because when two angles are equal then all three Angles must be equal.
2. SAS (Side-Angle-Side): Means we have two Triangles where:
- The ratio between two sides is the same as the ratio between the other two sides
- The included Angles are equal
For example:

From our example, we see that, the side AB corresponds to side XZ and side BC corresponds to side YZ, thus the ratios will be:
AB:XZ = 15:10 = 3:2 and
BC:YZ = 21:14 = 3:2
Also, there is a matching angle of750in between them.
The information is enough to tell us that the Triangles are Similar.
3. SSS (Side-Side-Side): Means we have three pairs of sides in the same ratio. Then the Triangles are Similar. For example;

In this example; the ratios of sides are:
a:x = 6:7.5 = 12:15 = 4:5
c:y = 4:5
b:z = 8:10 = 4:5
The ratios are all equal, so the Triangles are Similar.
Exercise 1
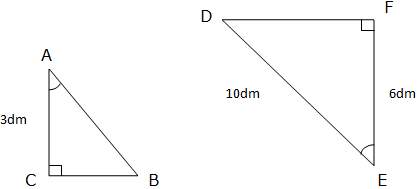
1. Use similarity to calculate side AB
2. ABC is a Triangle in which AC is produced to E and AB is Produced to D such that DE//BC. Show that AD:AB = DE:CB
3. Given Triangles ABC and PQR which are similar. If the lengths of sides AC = 4.8cm, AB = 4cm and PQ = 9cm find the length of side PR if side AB corresponds to PQ and BC corresponds to QR.
4. Prove that any two equilateral Triangles are similar.
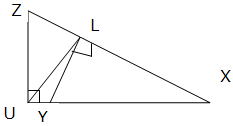
5. Name two similar triangles in the figure below:







EmoticonEmoticon