Join Our Groups
TOPIC 5: CONGRUENCE
I’m sure you have seen some of the figure which in one way or another one of the shape can become another using turns, flip or slide. These shapes are said to be Congruent. Study this notes carefully to know different ways that can help you to recognize congruent figures.
In geometry two figures or objects are congruent if they have the same shape and size, or if one has the shape and size as the mirror image of the other.
If one shape can become another using turns (rotation), flip (reflection), and/ or slide (translation), then the shapes are Congruent. After any of these transformations the shape must still have the same size, perimeters, angles, areas and line lengths.
Note that; the two shapes need to be the size to be Congruent i.e. only rotation, reflection and/ or translation is needed.
Remember this:
- Two line segments are Congruent if they have the same length.
- Two angles are Congruent if they have the same measure.
- Two circles are Congruent if they have the same diameter.
Angles formed by the intersection of two straight lines
When two straight lines intersect, they form four angles. Each opposite pair are called vertical angles and they are congruent. Vertical angles are also called opposite angles. See figure below for more understanding:
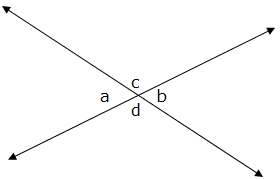
Properties of vertical angles
- They are Congruent: vertical angles are always of equal measure i.e. a = b, and c = d.
- Sum of vertical angles (all four angles) is 3600 i.e. a + b + c + d =3600
- Sum of Adjacent angles (angles from each pair) is 1800 i.e. a + d =1800 ; a + c =1800 ; c + b =1800 ; b + d =1800.
Congruence of Triangles
Two Triangles are Congruent if their corresponding sides are equal in length and their corresponding angles are equal in size. The symbol for congruent shapes is ≅
The Conditions for Congruence of Triangles
Determine the conditions for congruence of triangles
The following are conditions for two Triangles to be Congruent:
- SSS (side-Side-Side): if three pairs of sides of two Triangles are equal in length, then the Triangles are Congruent. Consider example below showing two Triangles with equal lengths of the corresponding sides.
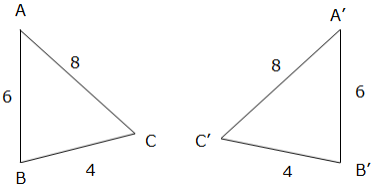
Example 1
Prove that the two Triangles (ΔABC and ΔBCD) below are Congruent.
Solution

Another condition;
- SAS (Side-Angle-Side): This means that we have two Triangles where we know two sides and the included angles are equal. For example;
If the two sides and the included angle of one Triangle are equal to corresponding sides and the included angle of the other Triangle, we say that the two Triangles are Congruent.
- ASA (Angle- Side-Angle): If two angles and the included side of one Triangle are equal to the two angles and included side of another Triangle we say that the two Triangles are congruence. For example
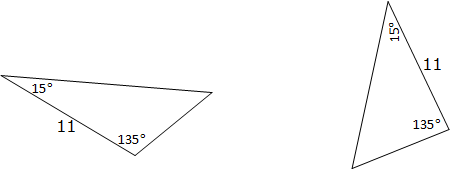
AAS condition;
- AAS (Angle-Angle-Side): If two angles and non included side of one triangle are equal to the corresponding angles and non included side of the other Triangle, then the two triangles are congruent. For example
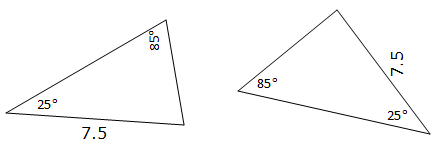
- HL (hypotenuse-Leg): This is applicable only to a right angled triangle. The longest side of a right angled triangle is called hypotenuse and the other two sides are legs.
It means we have two right angled triangles with:
- The same length of hypotenuse and
- The same length for one of the other two legs.
If the hypotenuse and one leg of one right angled triangle are equal to a corresponding hypotenuse and one leg of the other right angled triangle, the two triangles are congruent. For example

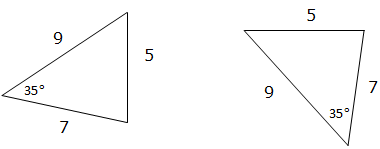
Important note: Do not use AAA (Angle-Angle-Angle). This means we are given all three angles of a triangle but no sides. This is not enough information to decide whether the two triangles are congruent or not because the Triangles can have the same angles but different size. See an illustration below:
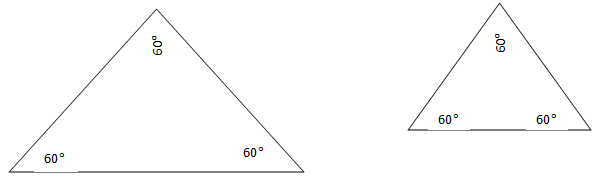
The two triangles are not congruent.
Without knowing at least one side, we can’t be sure that the triangles are congruent.
Congruence of Triangle
Prove congruence of triangle
Example 2
Prove that the two Triangles (ΔABC and ΔBCD) below are Congruent.

Solution;

Theorems on Congruence of Triangles to Solve Related Problems
Apply theorems on congruence of triangles to solve related problems
Isosceles Triangle Theorem
The figure below illustrates an example of an isosceles triangle:
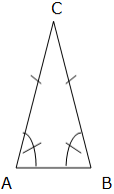
An isosceles triangle has two congruent sides (opposite sides) and two congruent angles. The congruent angles are called base angles and the other angle is called vertex angle. The angles A and B are base angles and angle C is the vertex angle.
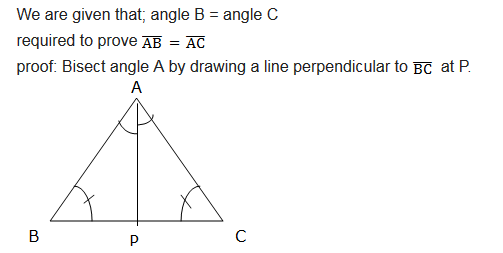
The base angle Theorem
If two sides of a triangle are congruent, then the angles opposite to these sides are congruent
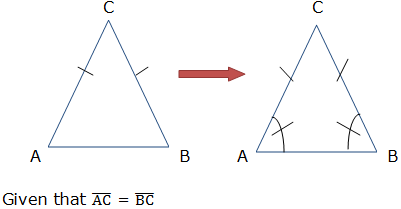
Required to prove: angle A = angle B

Therefore, the base angles i.e. angle CAS and angle BCS are equal (by the definition of a congruence of triangles).
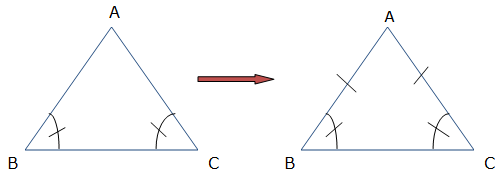
It states that, if two angles of a triangle are congruent, then sides opposite those angles are congruent.

Exercise 1
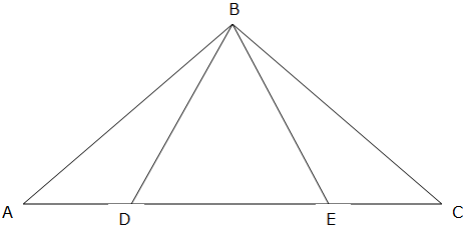
1. In the isosceles triangle ABC, BA and BC are congruent. D and E are points on AC such that AD is congruent to BD and BE is congruent to BC. Show that the triangles ABD and CBE are congruent
2. ABCD is a parallelogram and BEFC is a square. Show that triangles ABE and DCF are congruent.
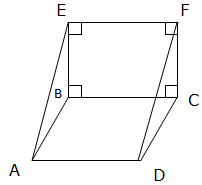
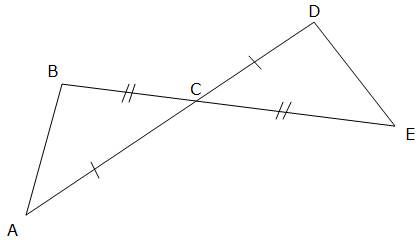
3. Use the figure below to answer the following questions:









EmoticonEmoticon