Join Our Groups
TOPIC 4: RATES AND VARIATIONS
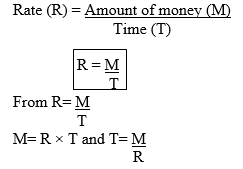


Rates
A rate is found by dividing one quantity by another.
Rates of Quantities of Different Kinds
Relate rates of quantities of different kinds
For example a rate of pay consists of the money paid divided by the time worked. If a man receives 1,000 shilling for two hours work, his rate of pay 1000 ÷ 2 = 500 shillings per hour. From the above example, we find out that
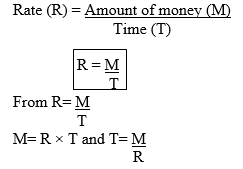
Example 1
1. A man is paid 6,000/= for 8 hours work.
- What is his rate of pay?
- At this rate, how much would he receive for 20 hours work?
- At this rate, how long must he work to receive 30,000 shillings?
Solution:


Quantities of the Same Kind
Relate quantities of the same kind
Example 2
A student is growing plants she measures the rate at which two of them are growing. Plant A grew 5cm in 10 days, and plant B grew 8cm in 12 days. Which plant is growing more quickly?
Exercise 1
1. A woman is paid 12,000/= for 8 hours work.
Converting Tanzanian Currency into other Currencies
Convert Tanzanian currency into other currencies
Different countries have different currencies. Normally money is changed from one currency to another using what is called a Rate of Exchange.
This makes trade and travel between countries convenient.
Conversion of money is done by multiplying or dividing by the rate of exchange.
Eg. If at a certain time there are 1,100 shillings to each UK pound (£), to go from £to shillings, multiply by 1,100, and to go from shillings to £divide by 1,100.
NB: The rate of exchange between two countries varies from time to time.
Example 3
Suppose the current rate of change between the Tanzanian shillings and the Euro is 650 Tsh per Euro.
- A tourist changes 200 euros to Tsh. How much does he get?
- A business woman changes 2,080,000 Tsh to euros. How much does she get?
Exercise 2
At a certain time there are 600 Tsh to one US dollar ($).
Variations
The Concept of Direct Variation
Explain the concept of direct variation
Some quantities are connected in such a way that they increase and decrease together at the same rate. For example if one quantity is doubled the other quantity is also doubled. These quantities are Directly Proportional or Vary Directly.
Eg. If a car is driven at a constant speed, the distance it goes is directly proportional to the time taken.
Also the amount of maize you buy is directly proportional to the amount of money you spend.
Problems on Direct Variations
Solve problems on direct variations
Example 4
1. Suppose different weights are hung from a wire. The extension of the wire is proportional to the weight hanging.
Suppose a weight of 2kg gives an extension of 5cm.
Find an equation giving the extension e cm in terms of weight w kg. Find the weight for an extension of 3cm.
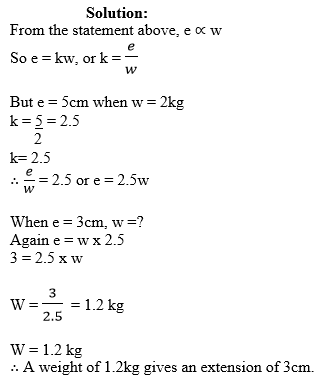
Example 5
Given that y is proportional to x such that, when x = 40, y = 5. Find an equation giving y in terms of x and use it to find (a) y when x = 15 (b) x when y = 20.
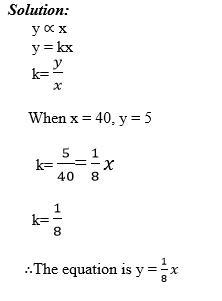
Example 6
The linear equation graph at the right shows that as the x value increases, so does the value increase for the coordinates that lie on this line.
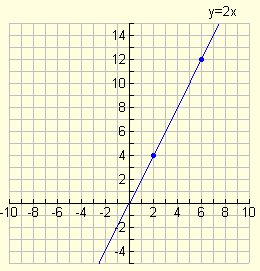
The Concept of Inverse Variation
Explain the concept of inverse variation
In some cases one quantity increase at the same rate as another decrease. For example, if the first quantity is doubled, the second quantity is halved.
In this case the quantities vary inversely, or they are inversely proportional. e.g. The number of men employed to dig a field is inversely proportional to the time it takes. Also the time to travel a journey is inversely proportional to the speed. We use the same symbol (∝) for proportionality.

Problems on Inverse Variations
Solve problems on inverse variations
Example 7
1. Suppose a mass of a gas is kept at a constant temperature. The volume of the gas is inversely proportional to its pressure.
If the volume is 0.8 m3 when the pressure is 250 N/m2, find the formula giving the volume in m3in terms of the pressure P N/m2. What is the volume when the pressure is increased to 1,000 N/m2?
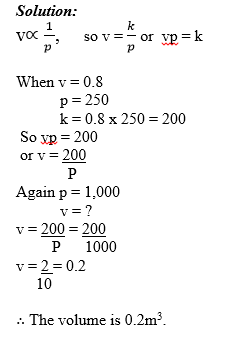
Example 8
Given that y is inversely proportional to x, such that x = 8 when y = 15. Find the formula connecting x and y by expressing y in terms of x and use it to find (a) y when x = 10, (b) x when y = 3
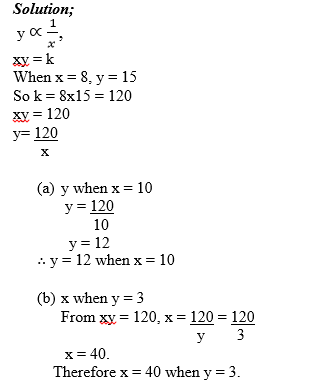
Exercise 3
The quantities p and q are inversely proportional to each other such that when q = 20, p=1.2
- Find the equation giving p in terms of q
- Find q when p = 0.5
- Find p when q = 160
Given that y is inversely proportional to x such that when y = 6, x =7. Find the equation connecting x and y by expressing x in terms of y and hence find x when y = 36
The number of workers needed to repair a road is inversely proportional to the time taken. If 12 workers can finish the repair in 10 days, how long will 30 workers take?
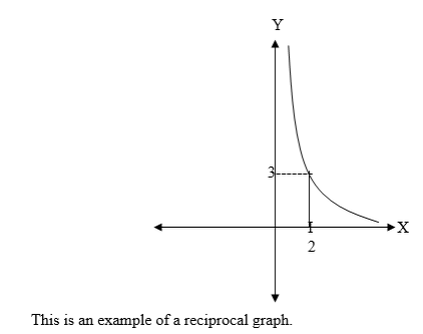
Graphs Relating Inverse Variations
Draw graphs relating inverse variations
The graph of y against x is shown for which y = 3 when x =2
Proportion to powers:
Sometimes a quantity is proportional to a power of another quantity. For example the area A of a circle is proportional to the square of its radius r,
So A ∝r2 or A= kr2

Example 9
1. The mass of spheres of a certain metal is proportional to the cube of their radii. A sphere of radius 10cm has mass 42kg. Find the formula giving the mass m kg in terms of radius r cm. Find the radius of the sphere with mass 5.25 kg.

Example 10
Given that M is proportional to the square of N and when N = 0.3, M = 2.7. Find the equation giving M in terms of N, and hence find the value of:
- M when N = 1.5
- N when M = 0.3
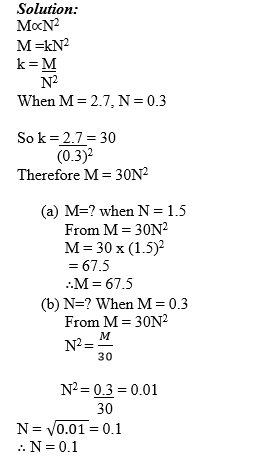
Joint Variation in Solving Problems
Use joint variation in solving problems
If a quantity varies as the product of two other quantities then it varies jointly with them. eg. If y = 3vu2, then y varies jointly with v and u2.
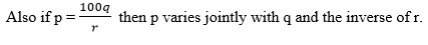
Example 11
1. Suppose a mass of a gas with volume Vm3 is under pressure P kg/m2 and has absolute temperature T0.
The volume of the gas varies jointly with its absolute temperature and inversely with its pressure. At a temperature of 300 k and pressure of 80kg/m2, the volume is 0.5m3. Find the formula for the volume in terms of T and P.
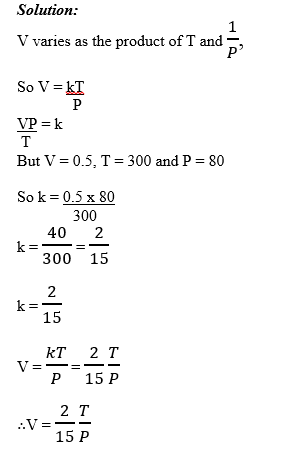
Example 12
m varies jointly with p and q such that when p = 12 and q = 5 then m= 15. Find m in terms of p and q and hence find m when P = 3 and q = 28
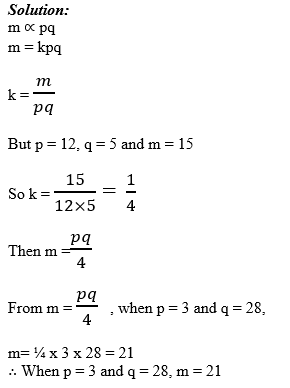
Exercise 4
1. M is inversely proportional to the cube of N, when N =2 then M = 20.
- Find an equation giving M in terms of N.
- Find M when N = 4
- Find N when M = 5.
2. P is inversely proportional to the square root of Q. When Q = 16 then P =5.
- Find an equation connecting P and Q expressing P in terms of Q.
- Find P when Q = 9
3. When a body is moving rapidly through the air, the air resistance R newtons is proportional to the square of the velocity Vm/s, At a velocity of 50m/s, the air resistance is 20N.
- Find R in terms of V
- Find the resistance at 100m/s.
4. B varies jointly with A and the inverse of C. When A = 3 and C = 12 then B = 20.
- Find B in terms of A and C.
- Find B when A = 8 and C= 2
5. The mass m kg of a solid wooden cylinder varies with the height h (m) and with the square of the radius r (m). If v = 0.2 and h = 1.4, then M = 150. Find m in terms of h and r.
Joint variation leading to areas and volumes
Many formulas for areas and volumes involve joint variation. For example the volume of a cylinder is given by v = πr2h.
So the volume varies jointly with the height and the square of the radius. i.e v∝r2h.
Example 13
1. A cylinder has radius 3cm and volume 10cm3. If the radius of the base is increased to 4cm without altering the height of the cylinder what effect does this have on the volume?

Example 14
A pyramid has a square base. If the height decreases by 10% but the volume remains constant, what must the side of the base increase by? (i.e What increase in the side will of set the decrease in the height?).

Exercise 5
1. A box has a square base of side 5cm. The volume of the box is 56cm3. If the sides increase by 10%, without the height changing, what is the new volume of the box?
2. A cone has volume 30cm3. If the radius increases by 10% and the height by 5%, what is the new volume of the cone?
3. A water tank holds 1,000 liters, and is in the shape of cuboids. The lengths of the sides of the base are enlarged by a scale factor of 1.4 without altering the height. What volume will the tank now hold?
4. The height of a cylinder is reduced by 20%. What percentage change is needed in the radius, if the volume remains constant?







Thanks your notes are very useful to me.!!
ReplyDelete