Join Our Groups
TOPIC 6: GEOMETRY
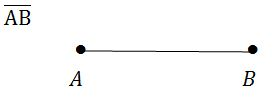


Points and Lines
The Concept of a Point
Explain the concept of a point
A point – is a smallest geometric figure which gives a position of object in a plane
A line segment – is a straight line joining two points in a plane
The Concept of a Point to Draw a Line
Extend the concept of a point to draw a line
A line segment – is a straight line joining two points in a plane

A line passing through two points e.g A and B and extends without end (i.e infinitely) in both directions is denoted by

The Difference Between a Line, a Line Segment and a Ray
Distinguish between a line, a line segment and a ray
A ray - is a line starting from a point, say A and pass through a point, say B and extends without end in one direction.It is denoted by

Angles and Lines
Angles
Draw angles
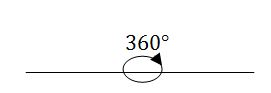
An angle – is a measure of an amount of turn. For instance, a complete turn has an angle of 360º
Measuring Angles of Different Size Using a Protractor
Measure angles of different size using a protractor
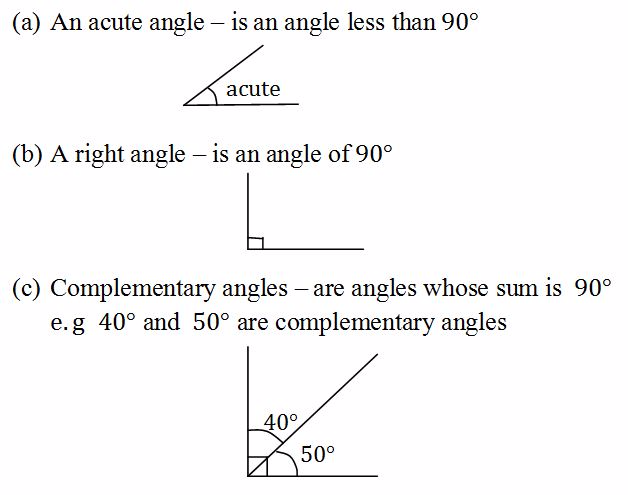
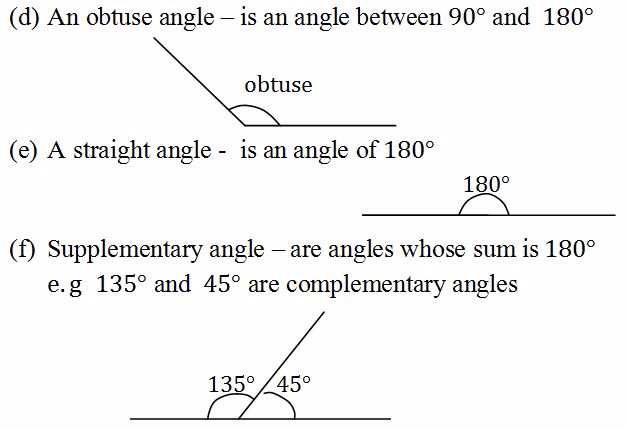
There are several types of angles including:- acute, right, complementary, obtuse, supplementary and reflex angle
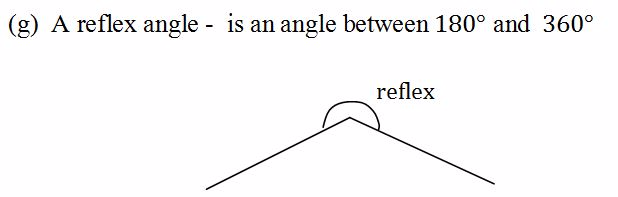
Example 1
- Two angles are supplementary. One angle is three times the other. What are the angles?
- Two angles are complementary. One angle is 40º greater than the other. What are the angles?
Solution
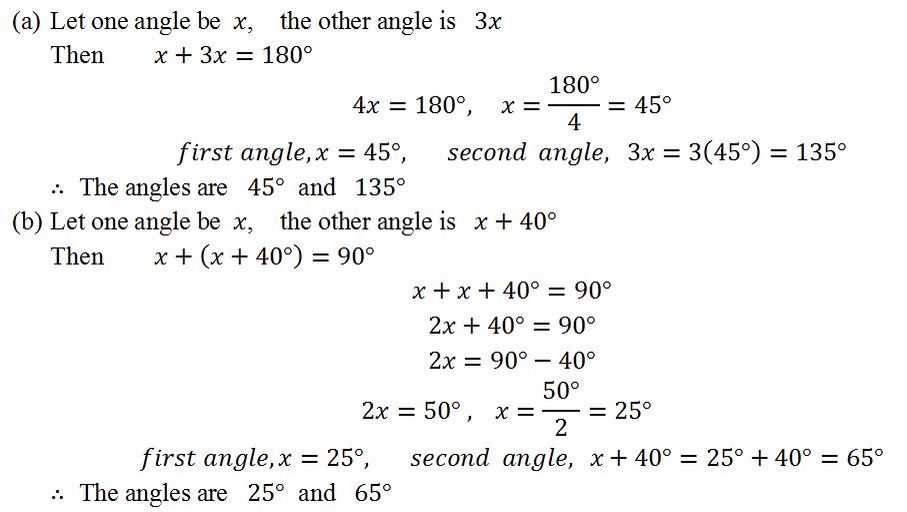
Drawing Angles Using a Protractor
Draw angles using a protractor
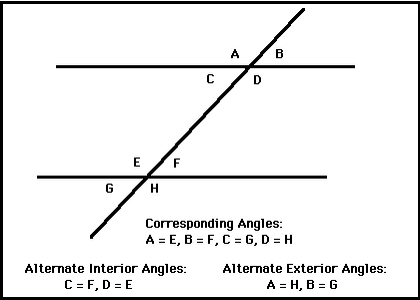
The angles formed by crossing lines includes vertically opposite angles, alternate angle and corresponding angles
Vertically opposite angles
The angles on the opposite sides of the crossing lines are equal
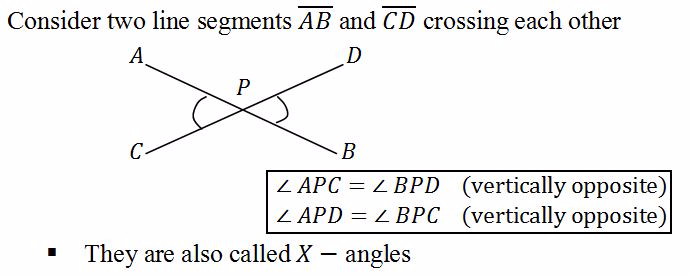
Alternate angles
Consider a line segment crossing two parallel line segments. This line is called a transversal
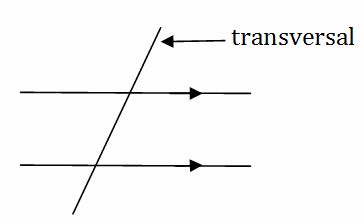
The angles within the parallel line segments on the opposite sides of the transversal are equal
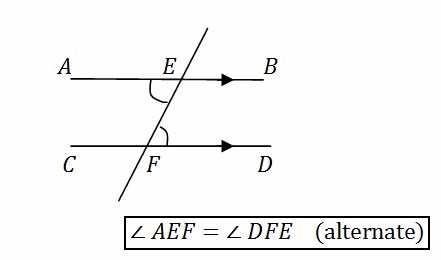
They are also called Z - angles
<!--[endif]-->Corresponding angles
The angles on the same side of the transversal and on the same side of the parallel lines are equal.They are called corresponding angles and sometimes called F - angles
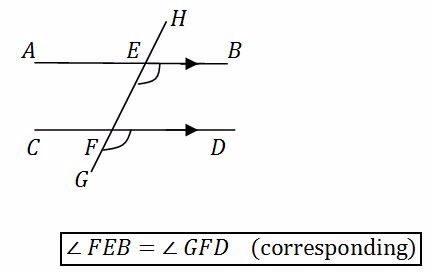
There are also three other pairs of corresponding angles in the diagram above.When showing that two angles are equal you must give reason whether they are vertically opposite, or alternate or corresponding angles.
Constructions
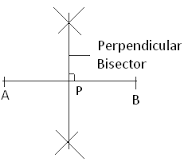
Construction of a Perpendicular Bisector to a Line Segment
Construct a perpendicular bisector to a line segment
Perpendicular Bisector to a Line Segment is shown below
Contruction of an Angle of 60° Using a Pair of Compasses
Construct an angle of 60° using a pair of compasses
Angle of 60°
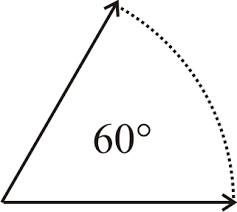
Bisection of a Given Angle
Bisect a given angle
Activity 1
Bisect a given angle
Copying a Given Angle by Construction
Copy a given angle by construction
Activity 2
Copy a given angle by construction
Parallel Lines
Construct parallel lines
Parallel lines can be shown as below:
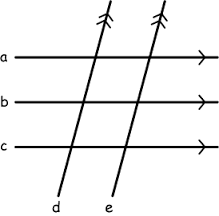
Different Types of Angles Formed by Parallel Lines and a Transversal
Identify different types of angles formed by parallel lines and a transversal
Different types of angles are shown below.
Polygons And Regions
A Polygon and a Region
Describe a polygon and a region
A polygon is a plane figure whose sides are three or more co planar segments that intersect only at their endpoints. Consecutive sides cannot be collinear and no more than two sides can meet at any one vertex.
A polygonal region is defined as a polygon and its interior.
Different Types of Triangles
Construct different types of triangles
A triangle – is a polygon with three sides.The sides connect the points called vertices.
A right – angled triangle – has one angle equal to 90º
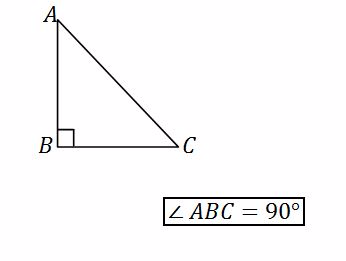
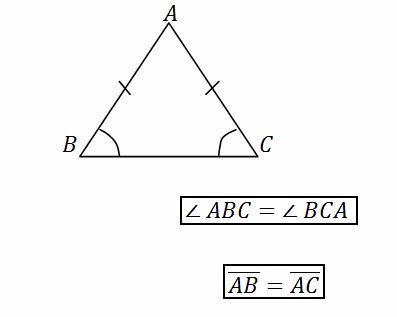
An isosceles triangle – has two equal sides and two equal angles
An equilateral triangle – has three equal sides and all angles equal
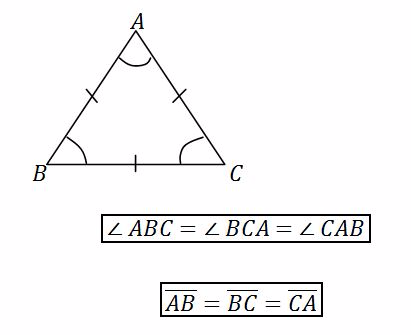
NOTE: A triangle with all sides different and all angles different is called scalene triangle.
A triangle with vertices A, B and C is denoted as
A triangle has two kinds of angles
- Interior angles
- Exterior angles
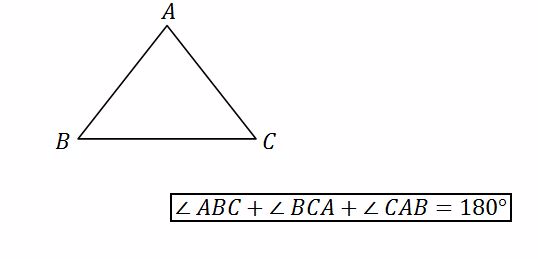
Interior angle – is an angle inside the triangle.The sum of interior angles of a triangle is 180.
Example, consider the triangle below
Exterior angle - is an angle outside the triangle. Consider the triangle below
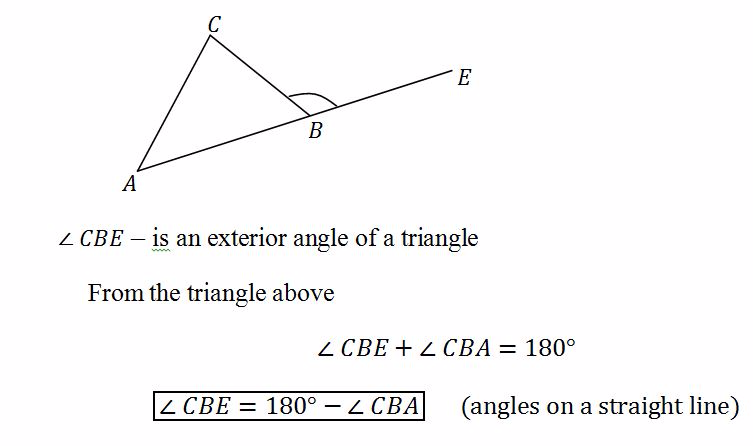
Example 2
Find the angles x and y in the diagrams below
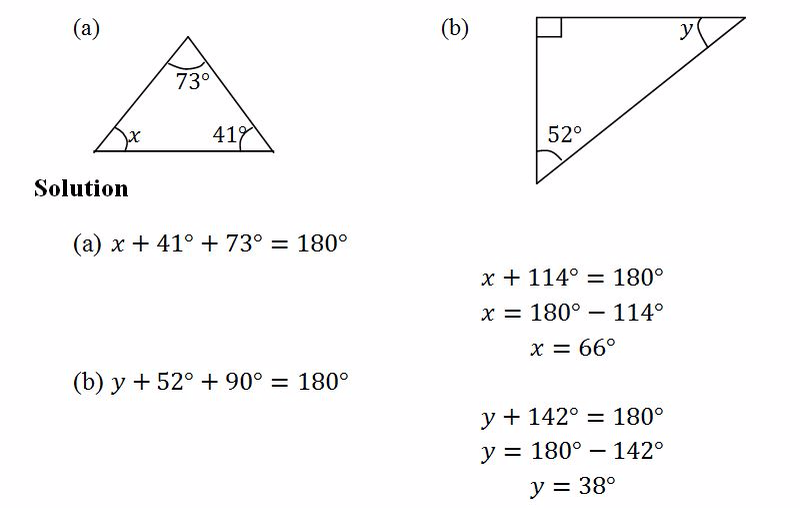
Different Quadrilaterals
Construct different quadrilaterals
A quadrilateral – is a polygon with four sides. Examples of quadrilaterals are a square, a rectangle, a rhombus, a parallelogram, a kite and a trapezium
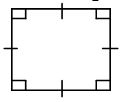
A square – has equal sides and all angles are 90º
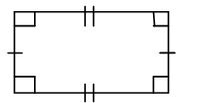
A rectangle – has two pairs of opposite sides equal and all angles are 90º
A rhombus – has all sides equal.Opposite angles are also equal
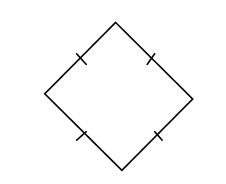
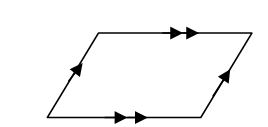
A parallelogram – has two pairs of opposite sides equal.Opposite angles are also equal
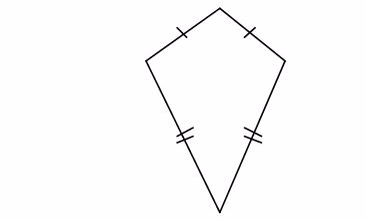
A kite – has two pairs of adjacent sides equal.One pair of opposite angles are also equal
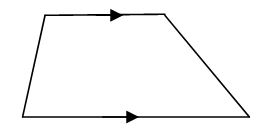
A trapezium – has one pair of opposite sides pair
Any quadrilateral is made up of two triangles. Consider the below quadrilateral.
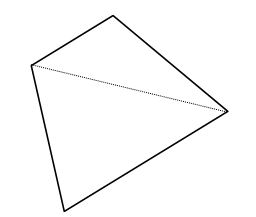
Sum of angles of quadrilateral = 2 ×180º = 360º
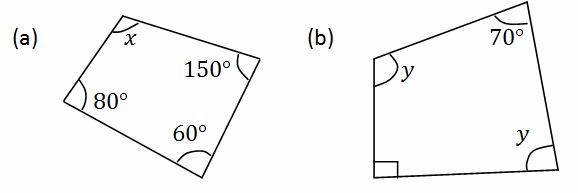
Example 3
Find the angles x and y in the diagrams below
Solution
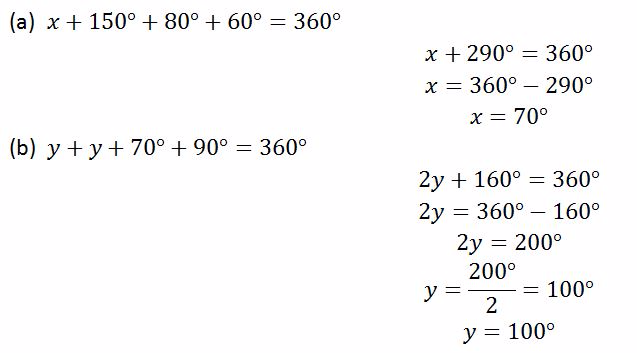
Circles
A Circle
Draw a circle
To make a circle: Draw a curve that is "radius" away from a central point.
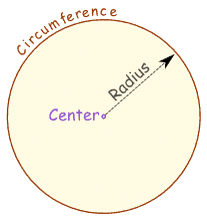
And so:All points are the same distance from the center.
You can draw it yourself: Put a pin in a board, put a loop of string around it, and insert a pencil into the loop. Keep the string stretched and draw the circle!
Different Parts of a Circle
Describe different parts of a circle
The radius of the circle is a straight line drawn from the center to the boundary line or the circumference. The plural of the word radius is radii.
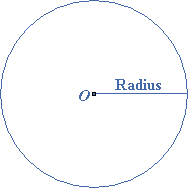
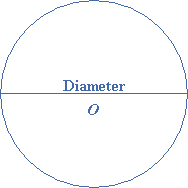
The diameter is the line crossing the circle and passing through the center. It is the twice of the length of the radius.
The circumference of a circle is the boundary line or the perimeter of the circle.

An arc is a part of the circumference between two points or a continuous piece of a circle. The shorter arc between P and Q is called the minor arc. The longer arc between Q and P is called the major arc.

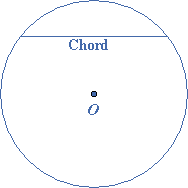
The chord is a straight line joining two points on the circumference points of a circle. The diameter is a special kind of the chord passing through the center.
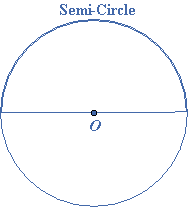
A semi-circle is an arc which is half of the circumference.
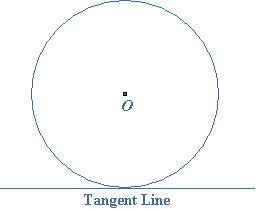
A tangent is a straight line which touches the circle. It does not cut the circumference. The point at which it touches, is called the point of contact.







EmoticonEmoticon