Join Our Groups
TOPIC 8: WORK, ENERGY AND POWER
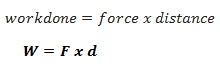
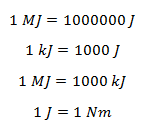
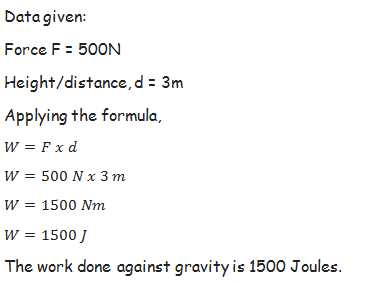

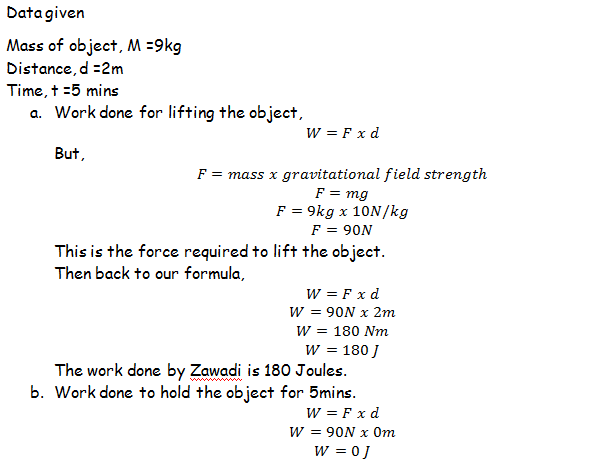
Work
The Concept of Work
Explain the concept of work
Work is said to be done only if the application of a force makes a body move from one point to another.
If a person pushes a wall and without making it move, even if the person sweat and physically become tired, he would not have done any work. But if the person pushes a trolley and the trolley moves then work is said to be done.
Work is defined as the product of the force applied and the distance moved in the direction of the force.
The S.I Unit of Work
State the S.I unit of work
Work is the product of force and distance moved in the direction of the force.
Thus,
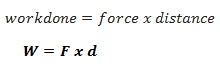
The SI unit of work done is Joule (J). Other units are Kilojoules (Kj) and megajoules (MJ) and Newton metre (Nm).
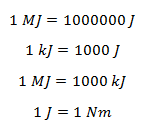
The Work Done by an Applied Force
Determine the work done by an applied force
The work will be done only if the following conditions are fulfilled; -
- There must be a force acting on a body.
- The body must move in a direction parallel to that of the applied force. That means, the direction movement of the object can be opposite to that of the applied force but parallel to it.
Therefore, work is NOT done if the force and distance are at right angle to each other (perpendicular).
Example 1
A sack of maize, which weighs 800N, is lifted to a height of 2m. What is work done against gravity?
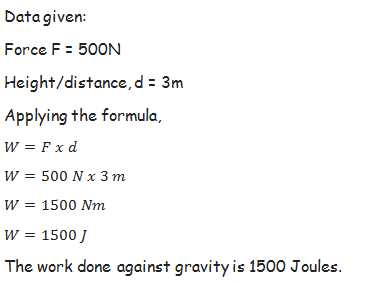
Example 2
A force of 70N pulls a box along a smooth and level ground a distance of 7m. Calculate the work done by force.

Example 3
Zawadi lifted a 9kg object 2m up and then hold it there for 5 minutes. How much work did Zawadi do for a) Lifting up the object, b) Holding the object for 5 minutes.
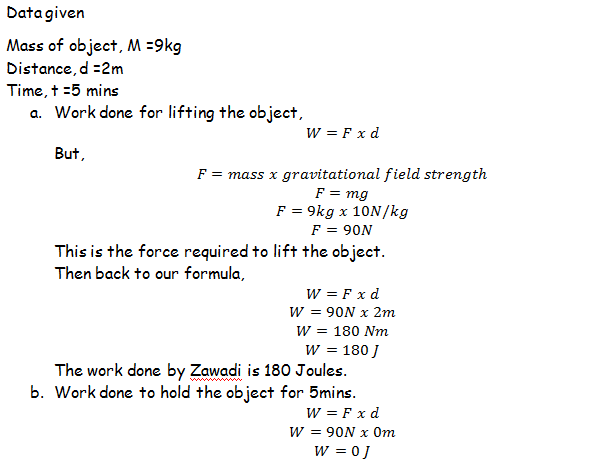
Energy
The Concept of Energy
Explain the concept of energy
Energy can be defined as capacity of doing work. It is the ability of doing work. In order for work to be done there must be a property which enables the act of doing work.
A person cannot move a box without having enough energy to do the work. Likewise, it is not possible for a car to move from one place to another without possessing some amount of energy to enable its movement.
S.I Unit of Energy
State S.I unit of energy
Energy and work done are closely related because energy is the property which make it possible for a certain work to be done. Therefore, Energy has the same SI unit like that of work, and that is Joules (J).
Different Forms of Energy
Identify different forms of energy
There are different forms of energy such as:
- Chemical energy
- Heat energy
- Light energy
- Sound energy
- Electrical energy
- Nuclear energy
- Solar energy
Difference between Potential Energy and Kinetic Energy
Distinguish between potential energy and kinetic energy
Potential energy and Kinetic energy are two forms of mechanical energy. Mechanical energy is the kind of energy which is associated with the position and motion of a body.
Potential energy – this is the energy possessed by the body due to its position. Its SI unit is Joules.
Potential energy of the body depends on its mass m, gravitational strength g, and the height h.
Suppose a body of 5 kg is at 2m above the ground and left to fall freely, the potential energy possessed by it before falling down is;
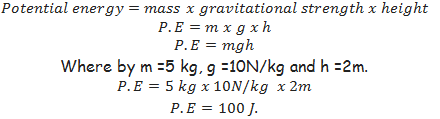
Kinetic energy – is the energy possessed by the body due to its motion. Its SI unit is Joules.
Kinetic energy of the body depends on its mass m and velocity, v.
A ball weighing 2kg kicked to attain velocity of 20 m/s possesses the Kinetic energy of;
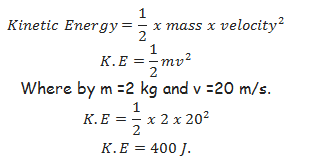
The Transformation of Energy
Explain the transformation of energy
The notion of energy is that energy is changed from one form into different forms using transducers.
Transducer is a device used to transform energy from one form to another.
For example:
- Battery converts chemical energy into electrical energy.
- A generator converts mechanical energy into electrical energy.
- A motor converts electrical energy into mechanical energy.
The Table Summarising Energy Transformation
| ORIGINAL ENERGY | TRANSDUCER | ENERGY OBTAINED |
| Chemical energy | Battery | Electrical energy |
| Electrical energy | Motor | Mechanical energy |
| Chemical energy | Generator | Electrical energy |
| Solar energy | Solar panel | Electrical energy |
| Chemical energy | Combustion engine | Mechanical energy |
| Sound energy | Microphone | Electrical energy |
| Electrical energy | Heater | Heat energy |
| Electrical energy | Speaker | Sound energy |
Activity 1
To demonstrate pressure of potential energy.
Materials and Apparatus
- A heavy stone
- A bucket full of water
- A strong inelastic rope; and
- Smooth pulley
Procedures:
- Collect the heavy stone, using a strong rope tie it to a bucket of water
- Pass the rope over smooth pulley fixed to a support.
- Hold stationary the heavy stone at height “h” above the ground
- Release the stone

Results and observations:
- When the stone released the bucket of water will start to rise.
- The stone is said to have potentials energy because of its position above the ground.
- Lifting a body of mass “m” to a height “h” above the ground requires work to be done against gravity. Work = Mgh
Example 4
A ball of mass 0.5 kg is kicked vertically upwards and rises to a height of 5m. Find the potential energy by the ball.
Data given:
Mass of the ball (Mb) = 0.5 kg
Height (h) = 5m
Gravitation force (g) 10N/kg
Potential energy (P.E) = ?
Solution:
Potential energy (P.E)= mgh
= 0.5kg x 10N/kg x 5m
= 25 NM
1NM= 1Joules
Potential energy (P.E) = 25 Joules.
Activity 2
Aim: to investigate the law of conservation of energy by a simple pendulum.
Materials and Apparatus:A pendulum bob and light inelastic string.
Producers
- Pull the bob of a simple pendulum in position A so that it is at height “h” above position B.
- Release the bob so that it swings to position C via the lowest position B and back to A.
- Consider the figure below:
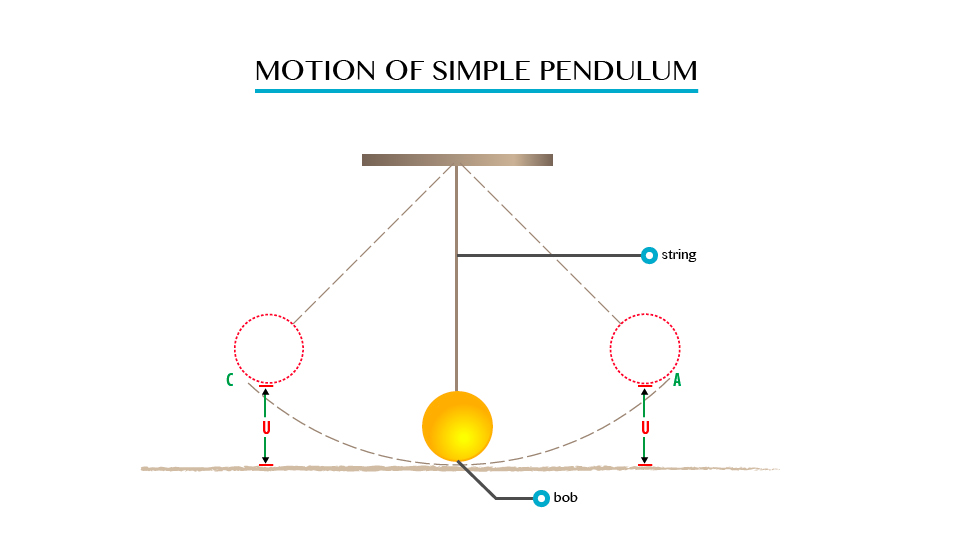
Observation
When the bob is at position A, it possesses potential energy only due to the height “h” which is equal to “Mgh”.
As it swings downwards to position B, the height decreases, and as the result it loses potential energy.
- The bob has Vmax and hence K.Emax at B. The height at B is zero, thus the P.E is zero.
- As it swings towards C, the P.E increases and reaches its maximum again in position C, where the Kinetic Energy is zero. At position D, the energy of the bob is party potential and party Kinetic.
The Principle of Conservation of Energy
State the principle of conservation of Energy
The energy which is already cycling in the universe can never be removed or it is impossible to create a new amount of energy in the universe. That is the energy is keeping in changing from one form to another.
This is well described by the principal of conservation of energy which states that; Energy is never created or destroyed but can be transformed from one form to another.
When a football player kicks the ball, the energy from his body is absorbed by the ball and transformed into Kinetic energy which makes the ball moves, sound energy which is heard during the kicking and small amount of heat energy.
Therefore, the amount of energy remains constant all the time.
Example 5
A stone of mass 2kg is released form a height of 2m above the ground. Find the potential energy of the stone when it is at the height of 0.5m above the ground.
Data given;
Mass of the stone (Ms) = 2kg
Height released (h) = 2m
Gravity (g) = 10N/kg
Potential energy = (P.E) ?
Solution:
P.E at height g 2m
P.E = Mgh
= 21g x 10N/kg x 2m
P.E = 40 Joules
P.E at 2m = 40Joules
Than P.E at height of 0.5m
= 21g x 10N/kg x 0.5m
P.E at 0.5m = 10Joules
100s of P.E = 40 Joules - 10Joules
= 30 Joules
According to conservation of energy the loss of P.E should be equal to the gain in K.E, when the air resistance is neglected.
K.E of the stone at 0.5 above the ground = 30 Joules
Example 6
A ball of mass 0.21kg is dropped from a height of 20m. on impact with the ground it loses 30J of energy. Calculate the height which it reaches on the rebound.
Data given;
Mass of ball (Mb) = 0.2kg
Height dropped (h) = 20m
Loose in energy (E) 30J
Height which reaches=?
Solution;
Consider the figure below;
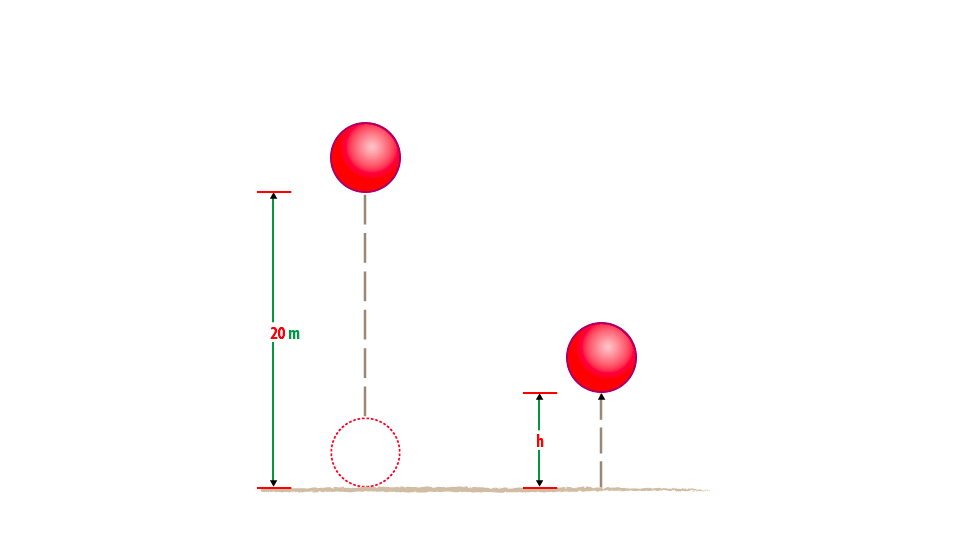
At 20m above ground the initial energy of the ball = Mgh
= 0.2kg x 10N/kg x 20m
= 40 Joules.
So after the impact the ball loose 30J and the energy remaining is 40 J-10J
= 10Joules
At the top of rebound the energy of the ball = potential energy (P.E)

The height reaches (h) is 5m.
Uses of Mechanical Energy
Explain the uses of mechanical energy
The mechanical energy can be used to produce electric power using generators. Some uses of mechanical energy are: It enables our body to do work, it makes work easier and faster, it is used to transport goods and people from one place to another, many transport vehicles uses the knowledge of mechanical energy. Examples of vehicles which uses mechanical energy are aeroplanes and motor cars.
Power
The Concept of Power
Explain the concept of power
Power is defined as the rate of which work is done. It measures the rate at which energy has been consumed. It is the measure of the rate at which the energy is changing.
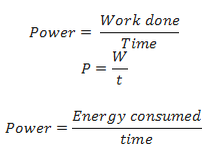
The S.I Unit of Power
State the S.I unit of power
The SI unit of power is Joule per second (J/s) which is also known as Watts (W).
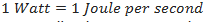
Other units of power are kilowatts (kW), megawatts (MW) and horsepower (hp).
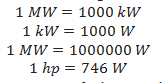
Watt is famously used for measurement of electrical power.
The Rate of Doing Work
Determine the rate of doing work
The rate of doing work is determined by how much little time is used to do a certain work.
If two machines A and B are performing an equal amount of work and at the end machine A uses more time than machine B to complete the work, then, machine B is considered to be powerful than machine A. This is because machine B took little time than machine B to do the same amount of work.
For example, two people are climbing up the stairs. One is climbing by running while the other is walking. Definitely, the person who is walking will take a longer time to reach at the top while the person who is running will take a shorter time. In this case, the person who is running up the ladder is considered more powerful because he reached the top at a shorter time compared to the one who was walking.
Suppose, Bahati and Baraka were pushing two boxes each of 20kg towards a 5m distance on a smooth surface. Bahati completed the work after 5 seconds while Baraka used 10 seconds.
The work done by Bahati,
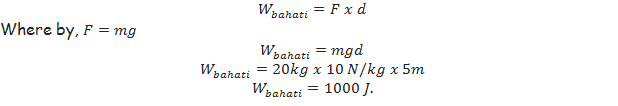
The work done by Baraka,<!--[endif]-->
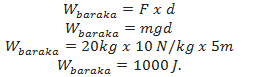
It can now be seen that both Bahati and Baraka did the same amount of work equal to 1000 Joules.
However, the power of Bahati and Baraka is not the same because they used different amount of time to complete the work. Hence, they differ in rate of doing work.
Power due to Bahati,
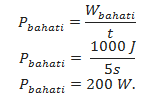
Power due to Baraka,
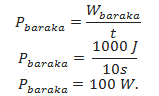
The above calculations show that Bahati’s rate of doing work is 200W while that of Baraka is 100W. Therefore, Bahati has more power than Baraka.
Example 7
How much power is required to accelerate a 1000kg car from rest to 26.7m/s in 8sec?
Solution:
The work done on the car increases its Kinetic energy.
Work done = AKE
½ MV2 – ½ MV2
The power required is given by:
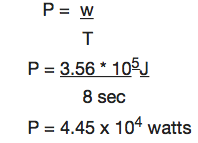
Example 8
Car engine is rated in horsepower (hp) where 1hp = 746watts. What is the required power measured in horsepower?
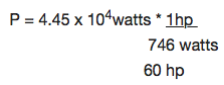
Since work causes a change in energy. DE power can be considered as the rate of change of energy.
P = DE/t







Physics form one past paper
ReplyDelete