Join Our Groups
TOPIC 4: THERMIONIC EMISSION
Thermionic emission is the discharge of electrons from heated materials, widely used as a source of electrons in conventional electron tubes (e.g., television picture tubes) in the fields of electronics and communications. The phenomenon was first observed (1883) by Thomas A. Edison as a passage of electricity from a filament to a plate of metal inside an incandescent lamp. The classical example of thermionic emission is the emission of electrons from a hot cathode into a vacuum (also known as thermal electron emission or the Edison effect) in a vacuum tube. The hot cathode can be a metal filament, a coated metal filament, or a separate structure of metal or carbides or borides of transition metals. Vacuum emission from metals tends to become significant only for temperatures over 1000 K. The science dealing with this phenomenon has been known as "thermionics," but this name seems to be gradually falling into disuse.
Cathode Rays
Cathode rays (also called an electron beam or e-beam) are streams of electrons observed in vacuum tubes.Electrons were first discovered as the constituents of cathode rays. In 1897 British physicist J. J. Thomson showed the rays were composed of a previously unknown negatively charged particle, which was later named the electron. Cathode ray tubes (CRTs) use a focused beam of electrons deflected by electric or magnetic fields to create the image in a classic television set.
The Production of Cathode Rays
Explain the production of cathode rays
Cathode rays are so named because they are emitted by the negative electrode, or cathode, in a vacuum tube. To release electrons into the tube, they first must be detached from the atoms of the cathode.
Modern vacuum tubes use thermionic emission, in which the cathode is made of a thin wire filament which is heated by a separate electric current passing through it. The increased random heat motion of the filament atoms knocks electrons out of the atoms at the surface of the filament, into the evacuated space of the tube.
Since the electrons have a negative charge, they are repelled by the cathode and attracted to the anode. They travel in straight lines through the empty tube. The voltage applied between the electrodes accelerates these low mass particles to high velocities. Cathode rays are invisible, but their presence was first detected in early vacuum tubes when they struck the glass wall of the tube, exciting the atoms of the glass and causing them to emit light, a glow called fluorescence.
Researchers noticed that objects placed in the tube in front of the cathode could cast a shadow on the glowing wall, and realized that something must be travelling in straight lines from the cathode.
After the electrons reach the anode, they travel through the anode wire to the power supply and back to the cathode, so cathode rays carry electric current through the tube. The current in a beam of cathode rays through a tube can be controlled by passing it through a metal screen of wires (a grid) to which a small voltage is applied.
The electric field of the wires deflects some of the electrons, preventing them from reaching the anode. Thus a small voltage on the grid can be made to control a much larger voltage on the anode. This is the principle used in vacuum tubes to amplify electrical signals.
High speed beams of cathode rays can also be steered and manipulated by electric fields created by additional metal plates in the tube to which voltage is applied, or magnetic fields created by coils of wire (electromagnets). These are used in cathode ray tubes, found in televisions and computer monitors, and in electron microscopes.

The Properties of Cathode Rays
State the properties of cathode rays
Properties of Cathode Rays Include:
- Cathode rays travel in straight lines. That is why, cathode rays cast shadow of any solid object placed in their path. The path cathode rays travel is not affected by the position of the anode.
- Cathode rays consist of matter particles, and posses energy by the virtue of its mass and velocity. Cathode rays set a paddle wheel into motion when it is placed in the path of these rays one the bladder of the paddle wheel.
- Cathode rays consist of negatively charged particles. When cathode rays are subjected to an electrical field, these get deflected towards the positively charge plate (Anode).We know that a positively charged body would attract only a negatively charged body, therefore the particles of cathode rays carry negative charge.Cathode rays also get deflected when these are subjected to a strong magnetic field.
- Cathode rays heat the object only which they fall. The cathode ray particles possess kinetic energy. When these particles strike an object, a part of the kinetic energy is transferred to the object. The causes a rise in the temperature of the object.
- Cathode rays cause green fluorescence on glass surface, i.e., the glass surface only which the cathode rays strike show a colored shine.
- Cathode rays can penetrate through thin metallic sheets.
- Cathode rays ionize the gases through which they travel.
- Cathode rays when fall only certain metals such as copper, but rays produced. The X-rays are not deflected by electrical or magnetic fields. X-rays pass through opaque materials such as black paper, but stopped by solid objects such as bones.
- Cathode rays travel with speed nearly equal to that of light.
The Application of Cathode Ray Tube
State the application of cathode ray tube
Application of cathode ray tube includes:
Televisions
Before LCD or Plasma television, the CRT was used to create a moving image.It used the same principle as a CRT, and for Black and White televisions, that worked fine. B&W TVs were essentially the same thing as a CRT, as all that's needed is the control of the brightness of the beam.
A CRT TV works by having the electron beam "scan" the screen at an rate faster than our eyes can perceive.This means that it shoots across the screen like a machine gun, and the images we see are actually made from many fluorescent dots.
The fluorescence caused by the beam striking the screen lasts a bit longer so that the next scan can be made without the previous image disappearing.It scans twice each time, first filling in the odd "holes" then the even ones.Each scan is about 1/50 of a second.
Colour CRT TVs had 3 electron guns rather than a single one, a shadow mask, and a modified fluorescent screen.The 3 electron guns were needed as there were three primary colours (Red, Green and Blue) that could be adjusted in different amounts to create any colour.
The colours are formed as a result of the shadow mask, which is a layer with holes in it that controls the angle of the incoming electron beams. This is because the fluorescent screen is separated into multi-coloured phosphors that are placed adjacent to each other at small intervals.
Thus it isn't actually a single coloured pixel, but rather 3 very small pixels that join together to form a larger dot.
Cathode Ray Oscilloscopes
Cathode ray oscilloscope is the device containing Cathode Ray Tube used to produce a beam of electrons and display graphs and patterns or signals on a screen. The patterns are displayed in horizontal and vertical axis (XY plane). The patterns may describe variations of voltage signals in waveforms.
A Cathode Ray Oscilloscope (CRO) is a diagnostic device that allows one to "see" voltage.It is essential a Cathode Ray Tube with two perpendicular sets of deflecting electric plates.The vertical set is where an input voltage is plugged in for the oscilloscope to display.
However, the horizontal set is connected to a 'sweep generator'.This is what provides a constant, but adjustable, time-base for the sweeping.It essentially creates a 'saw-tooth voltage'. This is what causes the image to be animated, and measured with a linear scale.
X-Rays
The Structure and Mode of Action of the X-ray Tube
Describe the structure and mode of action of the x-ray tube
X-radiation (composed of X-rays) is a form of electromagnetic radiation. Electromagnetic radiation (EM radiation or EMR) is a form of radiant energy released by certain electromagnetic processes. Visible light is one type of electromagnetic radiation, other familiar forms are invisible electromagnetic radiations such as X-rays and radio waves.
Most X-rays have a wavelength ranging from 0.01 to 10 nanometers, corresponding to frequencies in the range 30 pentahertz to 30 exahertz (3×1016 Hz to 3×1019 Hz) and energies in the range 100 eV to 100 keV.X-ray wavelengths are shorter than those of UV rays and typically longer than those of gamma rays.
In many languages, X-radiation is referred to with terms meaning Röntgen radiation, after Wilhelm Röntgen, who is usually credited as its discoverer, and who had named it X-radiation to signify an unknown type of radiation.
X-ray tube
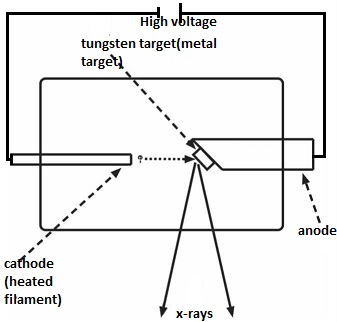
It is a special tube used to generate x-rays by generating accelerated electrons into highly energetic particles before they strike a metal target. Therefore, the highly energetic electrons are converted into x-rays after heating the metal target.
The x-ray tube consists of an emitter (either a filament or a cathode),which emits electrons into a vacuum and an anode to accelerate the electrons. This establishes a flow of electrons through the tube.
These electrons are reffered to as a beam. The cathode is in the form of a filament which emits electrons when heated. The anode is made of copper and also carries the target.
A high p.d between the anode and the cathode is maintained by an external high-voltage source. A battery that supplies high current is used to heat the cathode filament, which in many cases is made of tungsten. The cathode is in the form of a coil to provide high resistance to the passing current.
Production of X-rays
The electrons from the filament experiences the p. d and accelerated towards the anode. When they hit the anode, they are stopped and thereby transfer their energy to the electrons of the anode material. This gives rise to x-rays.
It is only a very small percentage of their energy that is converted to x-rays, with the rest of it being transformed to heat.
Defference between Soft and hard X-rays and their Production
Distinguish between soft and hard x-rays and their production
X-rays may be classified as hard or soft depending on their wavelengths, which give rise to different properties.
Differences between hard and soft x-rays
| Hard x-rays | Soft x-rays |
| They have shorter wavelength(high frequency) | They have longer wavelength |
| They have higher energy | Have less energy |
| Thigher penetrating power | Lower penetrating power |
| Are produced by higher accelerating potential | Produced by lower accelerating potential |
| Have higher velocity | Have lower velocity |
The Properties of X-rays
State the properties of x-rays
Properties of x-rays include:
- They travel in straight lines.
- They readily penetrate matter.
- They are not affected by electric or magnetic fields(they have no charge).
- They cause fluorescence in certain substances.
- They can be detected by photographic emulsion.
- They ionise gases causing the gases to conduct electricity.
The Application of X-Rays in Daily Life
Identify the applications of x-rays in daily life
The following are some uses of x-rays:
- In the medical field
- Crystallography
- Astronomy
- X-ray microscopic analysis
- X-ray fluorescence
- Security installations
- Industries







EmoticonEmoticon