Join Our Groups
TOPIC 11: STATISTICS
Statistics is the study of the collection, analysis, interpretation, presentation and organization of data. Statistics helps to present information using picture or illustration. Illustration may be in the form of tables, diagrams, charts or graphs.
Statistics helps to present information using picture or illustration. Illustration may be in the form of tables, diagrams, charts or graphs.
Pictograms
Information by Pictograms
Display Information by pictograms
This is a way of showing information using images. Each image stands for a certain number of things.
Interpretation of Pictograms
Interpret pictograms
For example here is a pictograph showing how many apples were sold over 4 months at a local shop.
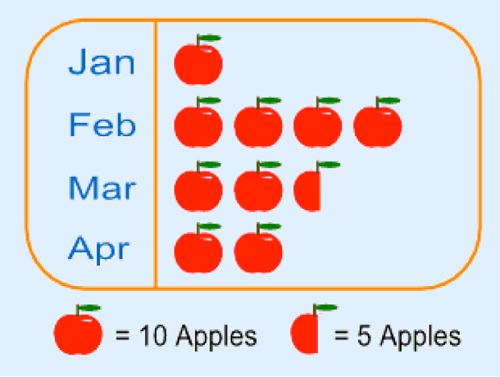
Each picture of 1 apple means 10 apples and the half-apple means 5 apples.
Note that:
- The method is not very accurate. For example in our example we can’t show just 1 apple or 2 apples.
- Pictures should be of the same size and same distance apart. This helps easy comparison.
- The scale depends on the amount of data you have. If the data is huge, then one image can stand for large number like 100, 1000, 10 000 and so on.
Bar Charts
They are also called bar graphs. Is a graphical display of information using bars of different heights.
Horizontal and Vertical Bar Charts
Draw horizontal and vertical bar charts
For example; imagine you just did a survey of your friends to find what kind of movie they liked best.
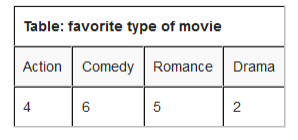
We can show that on a bar graph as here below:
Scale: vertical scale: 1cm represents 1 kind of movie
Horizontal scale: 1 cm represents 1 movie they watched.

Interpretation of Bar Chat
Interpret bar chart
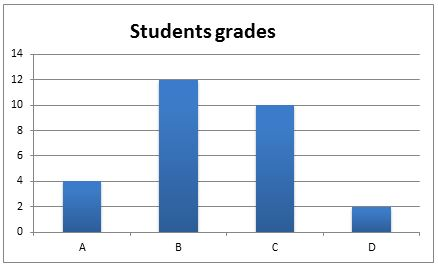
in a recent math test students got the following grades:

And this is a bar chart.
Scale: vertical scale: 1 cm represents 1 grade
Horizontal scale: 1 cm represents 2 students
Line Graphs
These are graphs showing information that is connected in some way. For example change over time.
Representing Data using Line Graphs
Represent data using line graphs
Example 1
you are learning facts about mathematics and each day you do test to see how Good you are.

Solution
We need to have a scale that helps us to know how many Centimeter will represent how many facts that you were correct.
Vertical scale: 1 cm represents 2 facts that you were right
Horizontal scale: 2 cm represents 1 day.

Interpretation of Line Graphs
Interpret line graphs
Example 2
The graph below shows the temperature over the year:
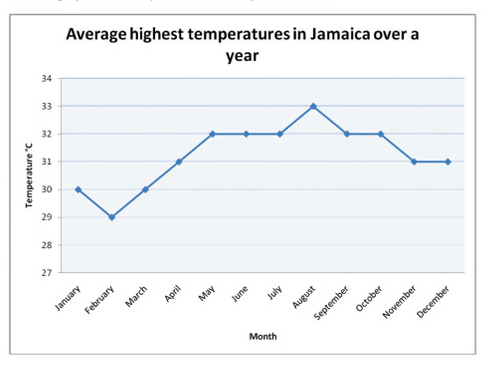
From the graph we can get the following data:
- The month that had the highest temperature was August.
- The month with the lowest temperature was February.
- The difference in temperature between February and may is (320-290)=30C.
- The total number of months that had temperature more than 300C was 9.
Pie Chart
This is a special chart that uses “pie slices” to show relative size of data. It is also called Circle graph.
Data using Pie Charts
Display data using pie charts
Example 3
The survey about pupils interests in subjects is as follows: 30 pupils prefer English, 40 pupils refer French and 50 pupils prefer Kiswahili. Show this information in a pie chart.
How to make them?
Step 1: put all you are data into a table and then add up to get a total.

Step 2: divide each value by the total and then multiply by 360 degrees to figure out how many degrees for each “pie slice” (we call pie slice a sector) We multiply by 360 degrees because a full circle has a total of 360 degrees.
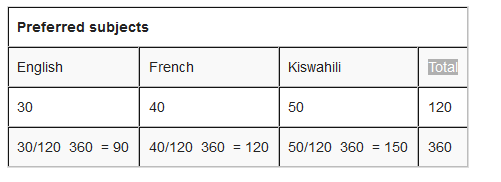
Step 3: draw a circle of a size that will be enough to show all information required. Use a protractor to measure degrees of each sector. It will look like the one here below:

Interpretation of Pie Charts
Interpret pie charts
Example 4
Interpreting the pie charts.
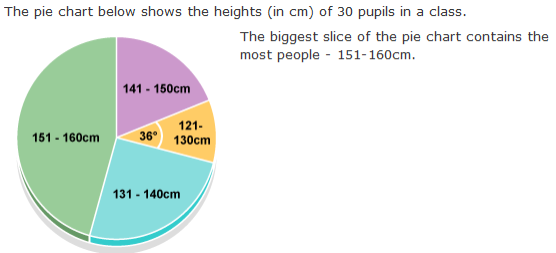
How many pupils are between 121-130cm tall?
The angle of this section is 36 degrees. The question says there are 30 pupils in the class. So the number of pupils of height 121 - 130 cm is:
36/360 x 30 = 3
Frequency Distribution Tables
Frequency is how often something occurs. For example; Amina plays netball twice on Monday, once on Tuesday and thrice on Wednesday. Twice, once and thrice are frequencies.
By counting frequencies we can make Frequency Distribution table.
Frequency Distribution Tables from Raw Data
Make frequency distribution tables from raw data
For example; Sam’s team has scored the following goals in recent games.
2, 3, 1, 2, 1, 3, 2, 3, 4, 5, 4, 2, 2, 3.
How to make a frequency distribution table?
•Put the number in order i.e. 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 5
•Write how often a certain number occurs. This is called tallying
- how often 1 occurs? (2 times)
- how often 2 occurs? (5 times)
- how often 3 occurs? (4 times)
- how often 4 occurs? (2 times)
- how often 5 occurs? (1 times)
•Then, wrote them down on a table as a Frequency distribution table.
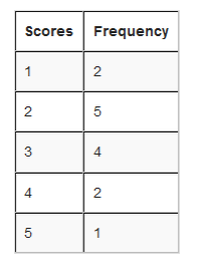
From the table we can see how many goals happen often, and how many goals they scored once and so on.
Interpretation of Frequency Distribution Table form Raw Data
Interpret frequency distribution table form raw data
Grouped Distribution Table
This is very useful when the scores have many different values. For example; Alex measured the lengths of leaves on the Oak tree (to the nearest cm)
9, 16, 13, 7, 8, 4, 18, 10, 17, 18, 9, 12, 5, 9, 9, 16, 1, 8, 17, 1, 10, 5, 9, 11, 15, 6, 14, 9, 1, 12, 5, 16, 4, 16, 8, 15, 14, 17.
How to make a grouped distribution table?
Step 1: Put the numbers in order. 1, 1, 1, 4, 4, 5, 5, 5, 6, 7, 8, 8, 8, 9, 9, 9, 9, 9, 9, 10, 10, 11, 12, 12, 13, 14, 14, 15, 15, 16, 16, 16, 16, 17, 17, 17, 18, 18,
Step 2: Find the smallest and the largest values in your data and calculate the range.
The smallest (minimum) value is 1 cm
The largest (maximum) value is 18 cm
The range is 18 cm – 1 cm = 17 cm
Step 3: Find the size of each group. Calculate an approximate size of the group by dividing the range by how many groups you would like. then, round that group size up to some simple value like 4 instead of 4.25 and so on.
Let us say we want 5 groups. Divide the range by 5 i.e. 17/5 = 3.4. then round up to 4
Step 4: Pick a Starting value that is less than or equal to the smallest value. Try to make it a multiple of a group size if you can. In our case a start value of 0 make the most sense.
Step 5: Calculate the list of groups (we must go up to or past the largest value).
In our case, starting at 0 and with a group size of 4 we get 0, 4, 8, 12, 16. Write down the groups. Include the end value of each group. (must be less than the next group):

The largest group goes up to 19 which is greater than the maximum value. This is good.
Step 6: Tally to find the frequencies in each group and then do a total as well.
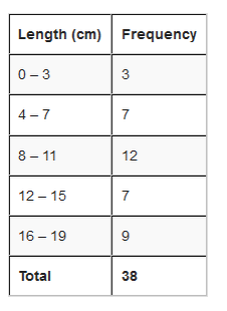
Done!
Upper and Lower values
Referring our example; even though Alex measured in whole numbers, the data is continuous. For instance 3 cm means the actual value could have been any were between 2.5 cm to 3.5 cm. Alex just rounded numbers to whole numbers. And 0 means the actual value have been any where between -0.5 cm to 0.5 cm. but we can’t say length is negative. 3.5 cm is called upper real limit or upper boundary while –0.5 cm is called lower real limit or lower boundary. But since we don’t have negative length we will just use 0. So regarding our example the lower real limit is 0.
The limits that we used to group the data are called limits. For example; in a group of 0 – 3, 0 is called lower limit and 3 is called upper limit.
See an illustration below to differentiate between Real limits and limits.
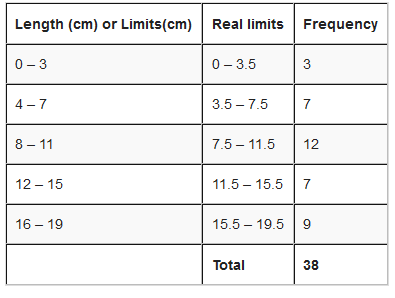
Class size is the difference between the upper real limit and lower real limit i.e. class size = upper real limit – lower real limit
We use the symbol N (capital N) to represent the total number of frequencies.
Class Mark of a class Interval
This is a central (middle) value of a class interval. It is a value which is half way between the class limits. It is sometimes called mid-point of a class interval. Class mark is obtained by dividing the sum of the upper and lower class limits by 2. i.e.
Class mark =
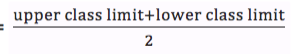
Referring to our example class marks for the class intervals are;
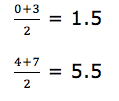
Interpretation of Frequency Distribution Tables
Interpret frequency distribution tables
Example 5
interpretation of frequency distribution data:
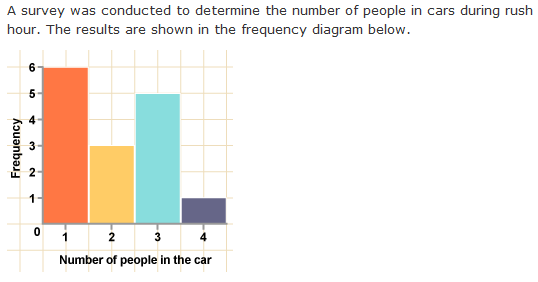
total number of cars in the survey:
6 + 3 + 5 + 1 = 15
There are 6 cars with one person in, 3 cars with two people, 5 cars with three people, and 1 car with four people.
the most likely number of people in a car:
Cars in the survey are most likely to have 1 person in them as this is the tallest bar - 6 of the cars in the survey had one occupant.
Frequency Polygons
This is a graph made by joining the middle-top points of the columns of a frequency Histogram
Drawing Frequency Polygons from Frequency Distribution Tables
Draw frequency polygons from frequency distribution tables
For example; use the frequency distribution table below to draw a frequency polygon.
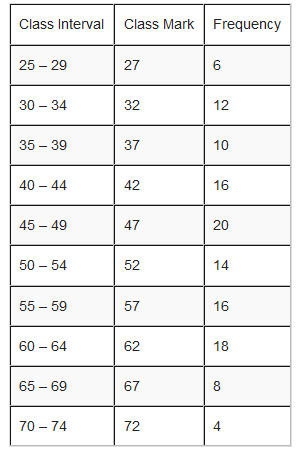
Solution
In a frequency polygon, one interval is added below the lowest interval and another interval is added above the highest interval and they are both assigned zero frequency. The points showing the frequency of each class mark are placed directly over the class marks of each class interval. The points are then joined with straight lines.
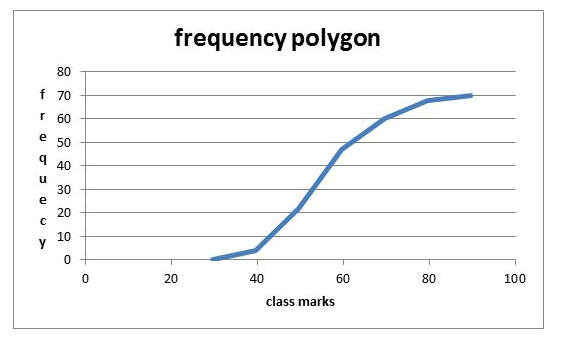
Interpretation of Frequency Polygons
Interpret frequency polygons
The frequency polygon below represents the heights, in inches, of a group of professional basketball players. Use the frequency polygon to answer the following questions:
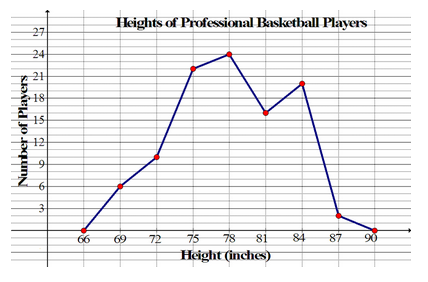
the number of players whose heights were measured 100.
Histograms
Is a graphical display of data using bars of different heights. It is similar to bar charts, but a Histogram groups numbers into ranges (intervals). And you decide what range to use.
Drawing Histograms from Frequency Distribution Table
Draw histograms from frequency distribution table
For example; you measure the height of every tree in the orchard in Centimeters (cm) and notice that, their height vary from 100 cm to 340 cm. And you decide to put the data into groups of 50 cm. the results were like here below:

Represent the information above using a histogram.
Solution
In order to draw histogram we need to calculate class marks. We will use class marks against frequencies.
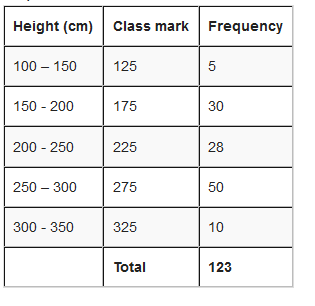
Scale: vertical scale: 1 cm represents 5 trees
horizontal scale: 1 cm represents 50 cm (range of trees heigths).
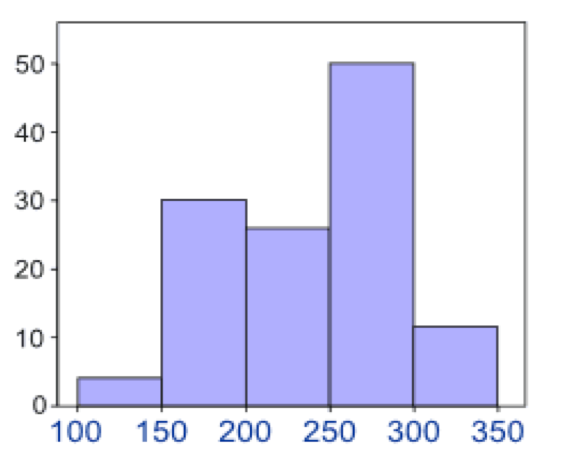
Interpretation of Histograms
Interpret histograms
The histogram below represents scores achieved by 250 job applicants on a personality profile.
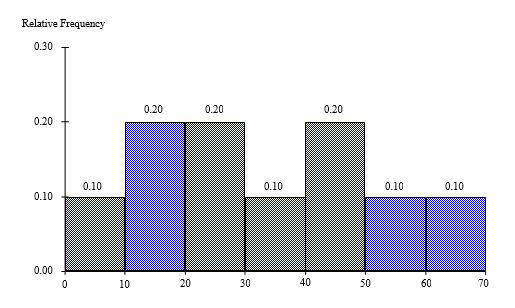
- Percentage of the job applicants scored between 30 and 40 is 10%
- Percentage of the job applicants scored below 60 is 90%
- Job applicants scored between 10 and 30 is 100
Cumulative Frequency Curves
Cumulative means “how much so far”. To get cumulative totals just add up as you go.
Drawing Cumulative Frequency Curves from a Cumulative Frequency Distribution Table
Draw cumulative frequency curves from a cumulative frequency distribution table
For example; Hamis has earned this much in the last 6 months.
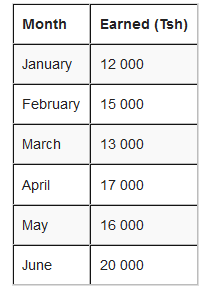
How to get cumulative frequency?
The first line is easy, the total earned so far is the same as Hamis earned that month.
But, for February, the total earned so far is Tsh 12 000 + Tsh 15 000 = Tsh 27 000.
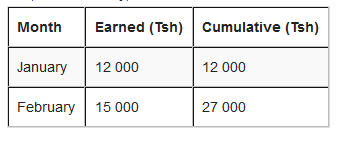
for March, we continue to add up. The total earned so far is Tsh 12 000 + Tsh 15 000 + Tsh 13 000 = 40 000 or simply take the cumulative of February add that of March i.e. Tsh 27 000 + Tsh 13 000 = Tsh 40 000.
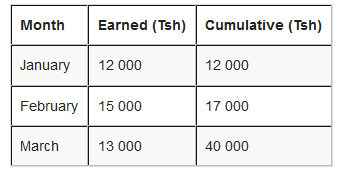
The rest of the months will be:
April: Tsh 40 000 + Tsh 17 000 = Tsh 57 000
May: Tsh 57 000 + Tsh 16 000 = Tsh 73 000
June: TSh 73 000 + Tsh 20 000 = Tsh 93 000
The results on a cumulative frequency table will be as here below:

The last cumulative total should math the total of all earnings.
Graph for cumulative polygon is drawn with cumulative frequency on vertical axis and real upper limits on Horizontal axis.
Scale: Vertical scale: 1cm represents Tsh 20 000
Give number to months. i.e. January =2, February =3 and so on
Note: To draw an Orgive, plot the points vertically above the upper real limits of each interval and then join the points by a smooth curve. Add real limit to the lowest real limit and give it zero frequency.
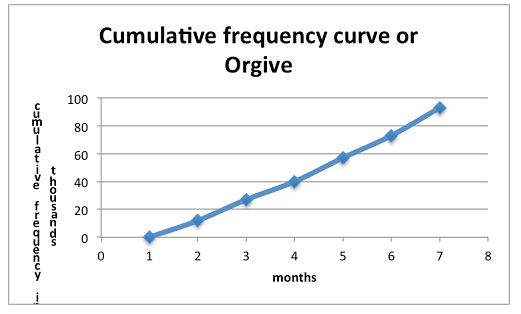
Interpretation of a Cumulative Frequency Curve
Interpret a cumulative frequency curve
Interpretation:
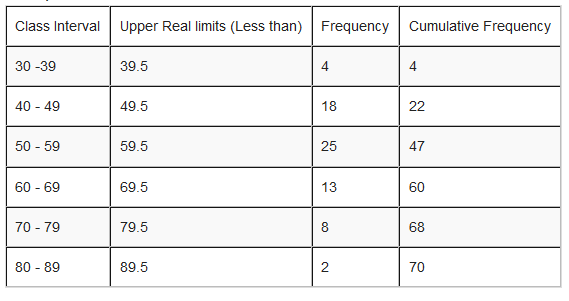
Its Cumulative Frequency Curve or Orgive will be:
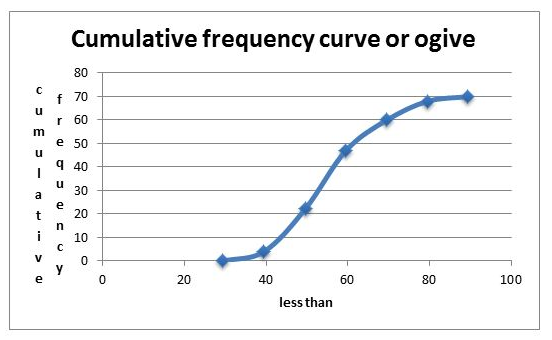
Exercise 1
1. Represent the data in the table below using pictures (pictograms)

2. The following table represent the number of pupils with their corresponding height.
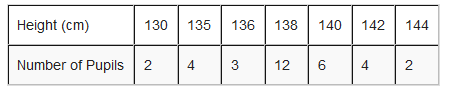
- How many pupils are less than 140 cm tall?
- What is the height of the tallest pupil?
- Present the data on a bar chart and on a line graph.
3. The following table shows the percentage of inflation in some countries in the year 2000.
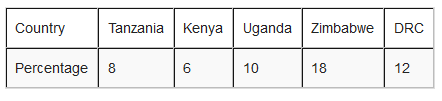
Represent the information on a pie chart.
4. Given the data below:
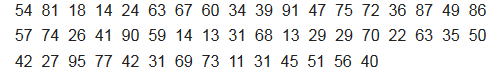
- Make a frequency distribution table with class intervals, real limits, and class marks. Use class size of 10.
- Construct: Histogram, Frequency Polygon and Ogive
State which class has highest frequency and which one has lowest frequency.







EmoticonEmoticon