Join Our Groups
TOPIC 2: FRACTIONS
A fraction is a number which is expressed in the form of a/b where a - is the top number called numerator and b- is the bottom number called denominator.
Proper, Improper and Mixed Numbers
A Fraction
Describe a fraction
A fraction is a number which is expressed in the form of a/b where a - is the top number called numerator and b- is the bottom number called denominator.
Consider the diagram below
The shaded part in the diagram above is 1 out of 8, hence mathematically it is written as 1/8
Example 1
(a) 3 out of 5 ( three-fifths) = 3/5
Example 2
(b) 7 0ut of 8 ( i.e seven-eighths) = 7/8
Example 3
- 5/12=(5 X 3)/(12 x 3) =15/36
- 3/8 =(3 x 2)/(8 X 2) = 6/16
Dividing the numerator and denominator by the same number (This method is used to simplify the fraction)
Difference between Proper, Improper Fractions and Mixed Numbers
Distinguish proper, improper fractions and mixed numbers
Proper fraction -is a fraction in which the numerator is less than denominator
Example 4
Proper fractions; 4/5, 1/2, 11/13
Improper fraction -is a fraction whose numerator is greater than the denominator
Example 5
Example of improper fractions are; 12/7, 4/3, 65/56
Mixed fraction -is a fraction which consist of a whole number and a proper fraction
Example 6
Mixed fractions
(a) To convert mixed fractions into improper fractions, use the formula below
(b) To convert improper fractions into mixed fractions, divide the numerator by the denominator
Example 7
Convert the following mixed numbers into improper fractions
Solution:
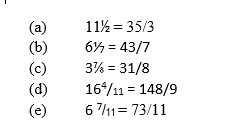
Example 8
Change 7/4 into a mixed number
Solution:
7/4 = 1¾
Example 9
Write the following fractions in order of size beginning with the smallest; 2/3, 5/6, 1/2, 3/4
Solution:
Change the fractions into decimals

Comparison of Fractions
In order to find which fraction is greater than the other, put them over a common denominator, and then the greater fraction is the one with greater numerator.
A Fraction to its Lowest Terms
Simplify a fraction to its lowest terms
Example 10
For the pair of fractions below, find which is greater
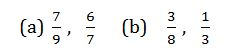
Solution
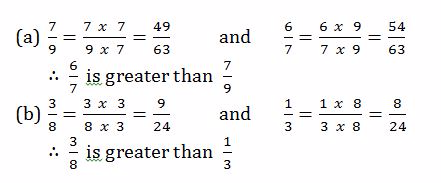
Equivalent Fractions
Identify equivalent fractions
Equivalent Fraction
- Are equal fractions written with different denominators
- They are obtained by two methods
Multiplying the numerator and denominator by the same number
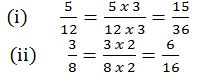
Give equivalent fractions to 1/4
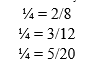
.
Dividing the numerator and denominator by the same number (this method is used to simplify the fraction)

NOTE: The fraction which cannot be simplified more is said to be in its lowest form
Example 11
Simplify the following fractions to their lowest terms
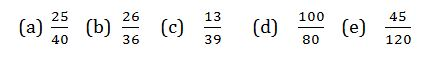
Solution

Fractions in Order of Size
Arrange fractions in order of size
Example 12
Arrange in order of size, starting with the smallest, the fraction
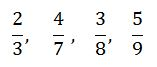
Solution
Change the fractions into decimals

Operations and Fractions
Addition of Fractions
Add fractions
Operations on fractions involves addition, subtraction, multiplication and division
- Addition and subtraction of fractions is done by putting both fractions under the same denominator and then add or subtract
- Multiplication of fractions is done by multiplying the numerator of the first fraction with the numerator of the second fraction, and the denominator of the first fraction with the denominator the second fraction.
- For mixed fractions, convert them first into improper fractions and then multiply
- Division of fractions is done by taking the first fraction and then multiply with the reciprocal of the second fraction
- For mixed fractions, convert them first into improper fractions and then divide
Example 13
Find
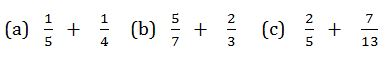
Solution
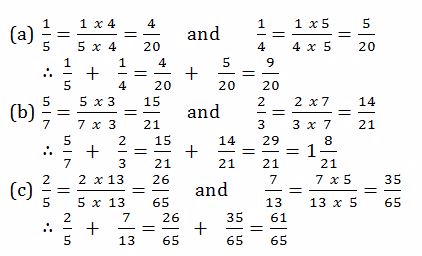
Example 14
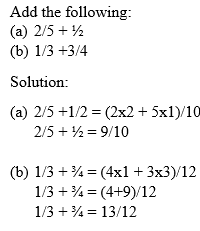
Subtraction of Fractions
Subtract fractions
Example 15
Evaluate
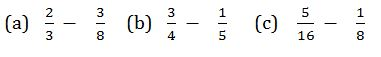
Solution
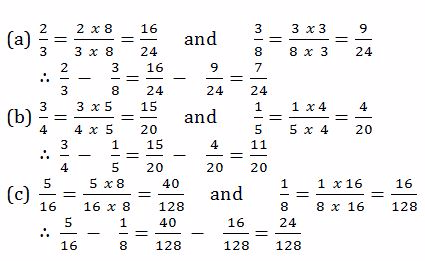
Example 16

Multiplication of Fractions
Multiply fractions
Example 17
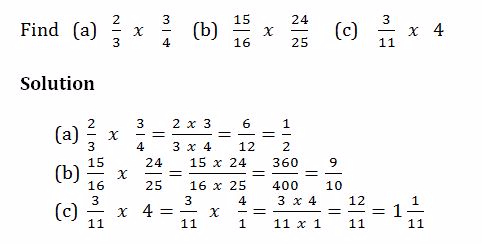
Division of Fractions
Divide fractions
Example 18
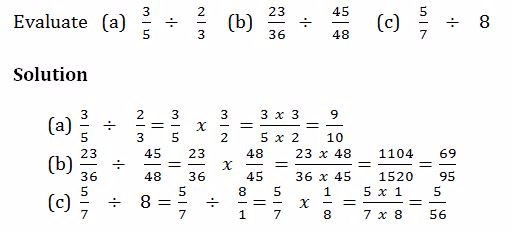
Mixed Operations on Fractions
Perform mixed operations on fractions
Example 19
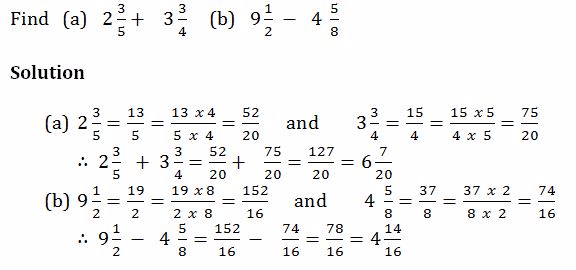
Example 20
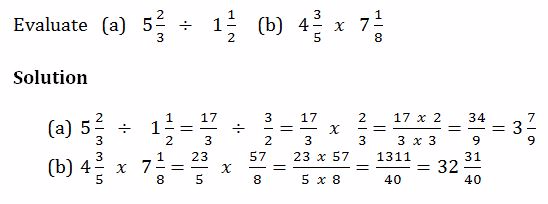
Word Problems Involving Fractions
Solve word problems involving fractions
Abdiel takes 2/3 of an hour to read 30 pages of a story book. How long does he take to read 1 page?
Solution:
1 page will take?
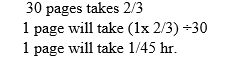
Example 21
Musa is 12 years old. His father is 3¾ times as old as he is. How old is his father?
Solution:
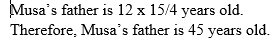
Example 22
1¾ metres of a material are needed to make a suit. How many suits can be made from 63 metres?
Solution:
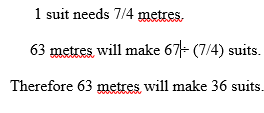







It would be better if you will add to each topic a working exercise. Thanks you have a lot of examples.
ReplyDeleteErnest Biseko
Ilemela Mwanza
thanks a lot it helps students during this quarantine
ReplyDeletethe system is so suitable in learning
ReplyDeleteWonderful
ReplyDeleteNi nzuri sana
ReplyDeleteZinarahisisha kazi kwa mwalimu nà mwanafunzi pia.
Àsante.