Join Our Groups
TOPIC 10: COORDINATE GEOMETRY


Coordinates of a Point
The Coordinates of a Point
Read the coordinates of a point
Coordinates of a points – are the values of 𝑥 and 𝑦 enclosed by the bracket which are used to describe the position of a point in the plane
The plane used is called 𝑥𝑦 − plane and it has two axis; horizontal axis known as 𝑥 − axis and; vertical axis known as 𝑦 − axis
A Point Given its Coordinates
Plot a point given its coordinates
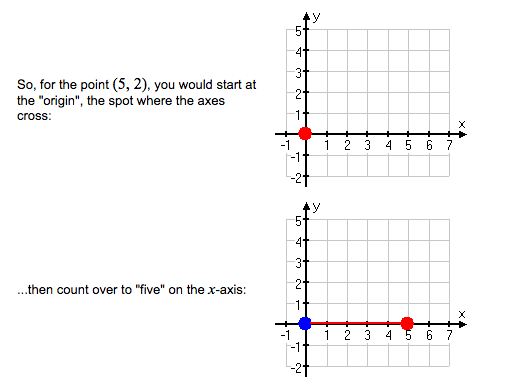
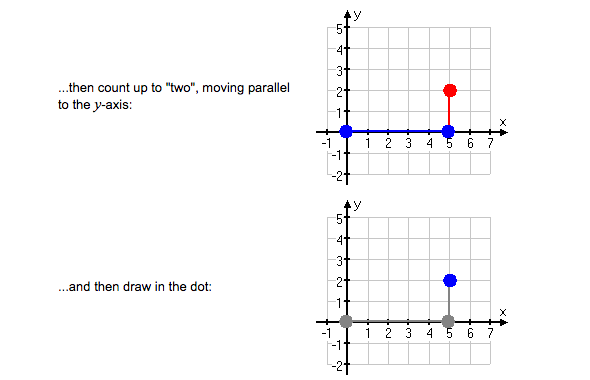
Suppose you were told to locate (5,2) on the plane. Where would you look? To understand the meaning of (5, 2), you have to know the following rule: The x-coordinate (always comes first). The first number (the first coordinate) is always on the horizontal axis.


A Point on the Coordinates
Locate a point on the coordinates
The location of (2,5) is shown on the coordinate grid below. Thex-coordinate is 2. They-coordinate is 5. To locate (2,5), move 2 units to the right on thex-axis and 5 units up on they-axis.

The order in which you writex- andy-coordinates in an ordered pair is very important. Th ex-coordinate always comes first, followed by they-coordinate. As you can see in the coordinate grid below, the ordered pairs (3,4) and (4,3) refer to two different points!

Gradient (Slope) of a Line
The Gradient of a Line Given Two Points
Calculate the gradient of a line given two points
Gradient or slope of a line – is defined as the measure of steepness of the line. When using coordinates, gradient is defined as change in 𝑦 to the change in 𝑥.
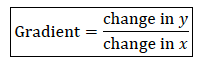
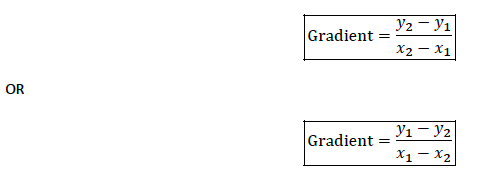
Consider two points 𝐴 (𝑥1, 𝑦1)and (𝐵 𝑥2, 𝑦2), the slope between the two points is given by:
Example 1
Find the gradient of the lines joining:
- (5, 1) and (2,−2)
- (4,−2) and (−1, 0)
- (−2,−3) and (−4,−7)
Solution
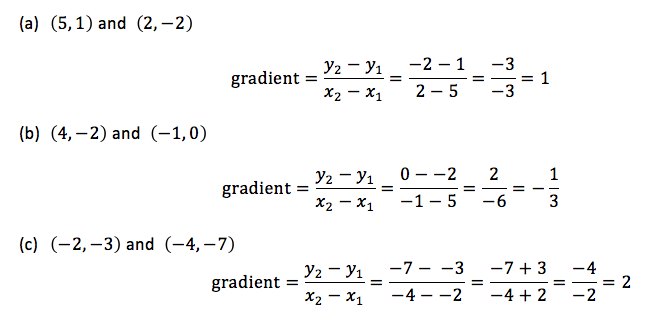
Example 2
- The line joining (2,−3) and (𝑘, 5) has gradient −2. Find 𝑘
- Find the value of 𝑚 if the line joining the points (−5,−3) and (6,𝑚) has a slope of½
Solution
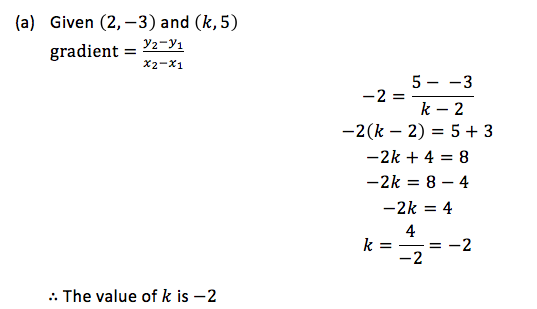
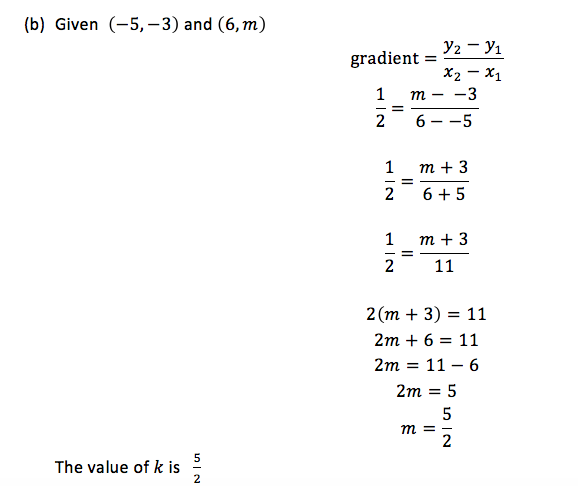
Equation of a Line
The Equations of a Line Given the Coordinates of Two Points on a Line
Find the equations of a line given the coordinates of two points on a line
The equation of a straight line can be determined if one of the following is given:-
- The gradient and the 𝑦 − intercept (at x = 0) or 𝑥 − intercept ( at y=0)
- The gradient and a point on the line
- Since only one point is given, then
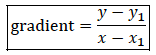
- Two points on the line
Example 3
Find the equation of the line with the following
- Gradient 2 and 𝑦 − intercept −4
- Gradient −2⁄3and passing through the point (2, 4)
- Passing through the points (3, 4) and (4, 5)
Solution
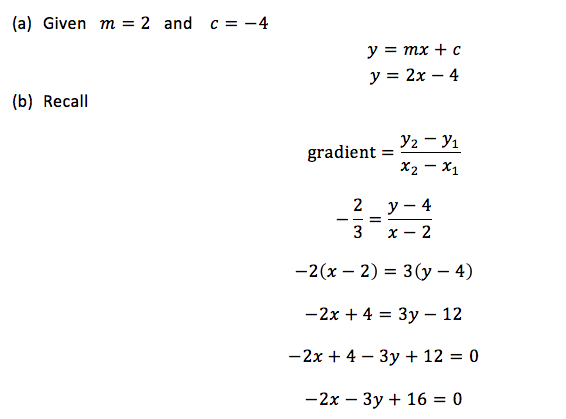
Divide by the negative sign, (−), throughout the equation
∴The equation of the line is 2𝑥 + 3𝑦 − 16 = 0

The equation of a line can be expressed in two forms
- 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0 and
- 𝑦 = 𝑚𝑥 + 𝑐
Consider the equation of the form 𝑦 = 𝑚𝑥 + 𝑐
𝑚 = Gradient of the line
Example 4
Find the gradient of the following lines
- 2𝑦 = 5𝑥 + 1
- 2𝑥 + 3𝑦 = 5
- 𝑥 + 𝑦 = 3
Solution

Intercepts
The line of the form 𝑦 = 𝑚𝑥 + 𝑐, crosses the 𝑦 − 𝑎𝑥𝑖𝑠 when 𝑥 = 0 and also crosses 𝑥 − 𝑎𝑥𝑖𝑠 when 𝑦 = 0
See the figure below
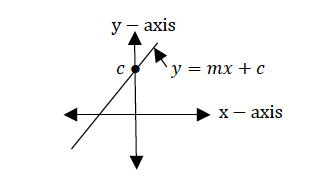
Therefore
- to get 𝑥 − intercept, let 𝑦 = 0 and
- to get 𝑦 − intercept, let 𝑥 = 0
From the line, 𝑦 = 𝑚𝑥 + 𝑐
𝑦 − intercept, let 𝑥 = 0
𝑦 = 𝑚 0 + 𝑐 = 0 + 𝑐 = 𝑐
𝑦 − intercept = c
Therefore, in the equation of the form 𝑦 = 𝑚𝑥 + 𝑐, 𝑚 is the gradient and 𝑐 is the 𝑦 − intercept
Example 5
Find the 𝑦 − intercepts of the following lines
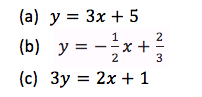
Solution

Graphs of Linear Equations
The Table of Value
Form the table of value
The graph of a straight line can be drawn by using two methods:
- By using intercepts
- By using the table of values
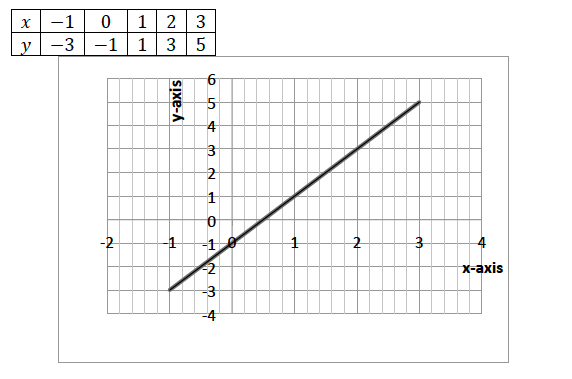
Example 6
Sketch the graph of 𝑦 = 2𝑥 − 1
Solution

The Graph of a Linear Equation
Draw the graph of a linear equation
By using the table of values
Simultaneous Equations
Linear Simultaneous Equations Graphically
Solve linear simultaneous equations graphically
Use the intercepts to plot the straight lines of the simultaneous equations. The point where the two lines cross each other is the solution to the simultaneous equations
Example 7
Solve the following simultaneous equations by graphical method
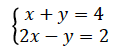
Solution
Consider: 𝑥 + 𝑦 = 4
If 𝑥 = 0, 0 + 𝑦 = 4 𝑦 = 4
If 𝑦 = 0, 𝑥 + 0 = 4 𝑥 = 4
Draw a straight line through the points 0, 4 and 4, 0 on the 𝑥𝑦 − plane
Consider: 2𝑥 − 𝑦 = 2
If 𝑥 = 0, 0 − 𝑦 = 2 𝑦 = −2
If 𝑦 = 0, 2𝑥 − 0 = 2 𝑥 = 1
Draw a straight line through the points (0,−2) and (1, 0) on the 𝑥𝑦 − plane
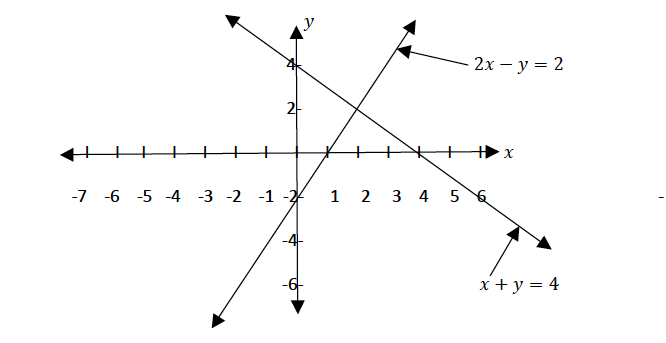
From the graph above the two lines meet at the point 2, 2 , therefore 𝑥 = 2 𝑎𝑛𝑑 𝑦 = 2
Exercise 1
1. Find the gradient of a line joining the points M(-3,1) and N(4,7).
2. Find the equation of a line which passes through (1,2) and a gradient of -3.
3. Given that the line y=2x+c passes through the point A(1,3). Find the value of c.
4. Find the gradient of a line joining points A(-1,2) and B(3,-2).
5. A straight line of a gradient 5 passes through the point B(3,-8). Find the equation of the line.
6. Draw the graph of the equation y = 4x+1: use the graph to answer the following questions.(a) What is the gradient? (b) What is the value of the y- intercept? (c) What is the value of y when x = -1?







EmoticonEmoticon