MATHEMATICS: FORM FOUR: Topic 5 - TRIGONOMETRY

 Join Our Groups

TELEGRAM | WHATSAPP

Schemes of Work 2024

Necta Timetables 2024

English Course - Free

Kenya Notes

TOPIC 5: TRIGNOMETRY

Trigonometry is a branch of mathematics that deals with relationship (s) between angles and sides of triangles.

Trigonometric Ratios

The Sine, Cosine and Tangent of an Angle Measured in the Clockwise and Anticlockwise Directions

Determine the sine, cosine and tangent of an angle measured in the clockwise and anticlockwise directions

The basic three trigonometrical ratios are sine, cosine and tangent which are written in short as Sin, Cos, and tan respectively.

Consider the following right angled triangle.

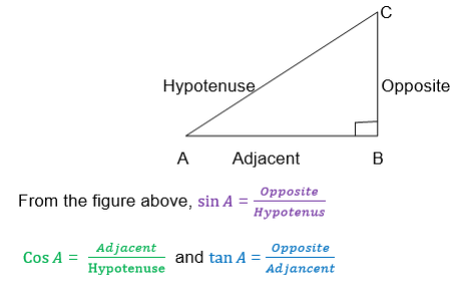
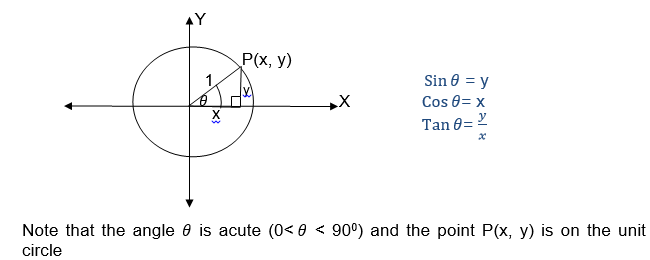
Also we can define the above triangle ratios by using a unit Circle centered at the origin.

If θis an obtuse angle (90⁰<θ<180⁰) then the trigonometrical ratios are the same as the trigonometrical ratio of 180⁰-θ

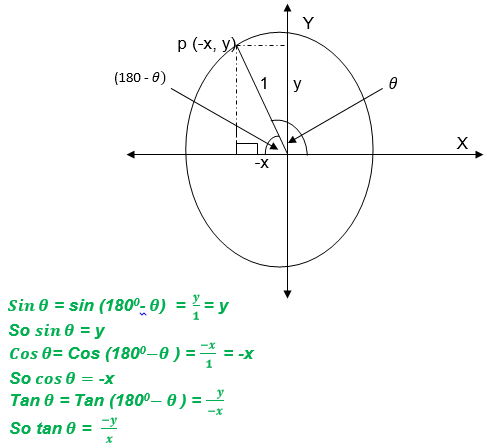
The angles are as given below

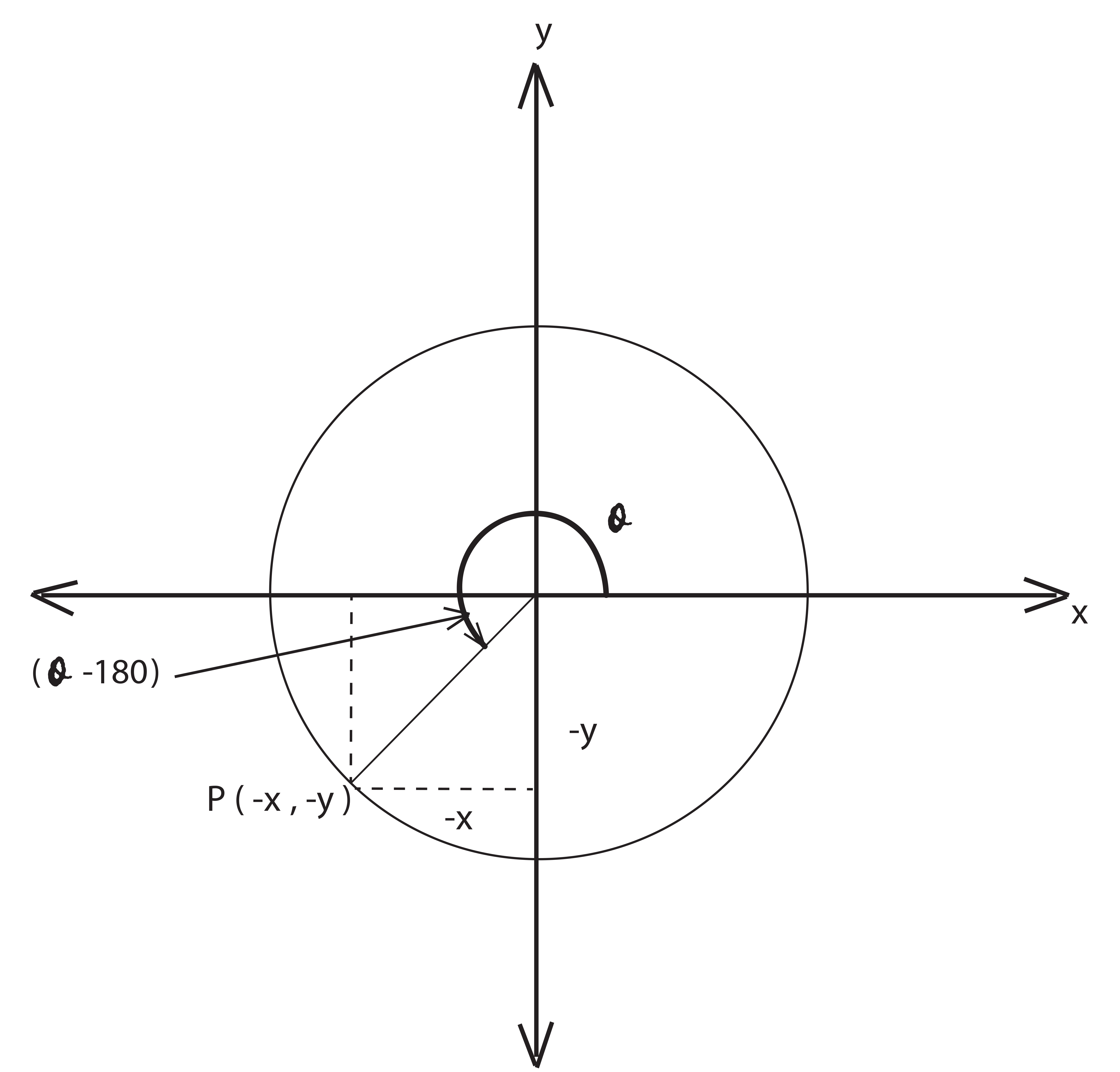
If θ is reflex angle (180<θ<270) then the trigonometric ratios are the same as that of θ-180

If θis a reflex angle (270⁰< θ< 360⁰), then the trigonometrical ratios are the same as that of 360⁰ -θ

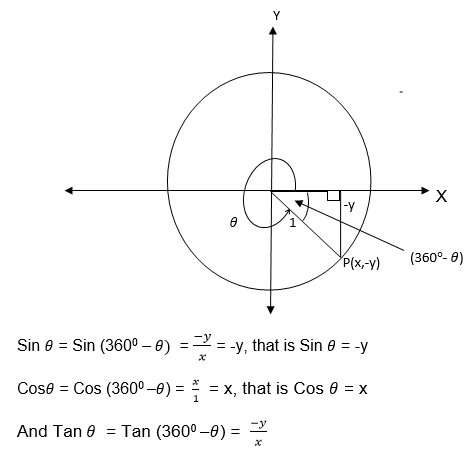
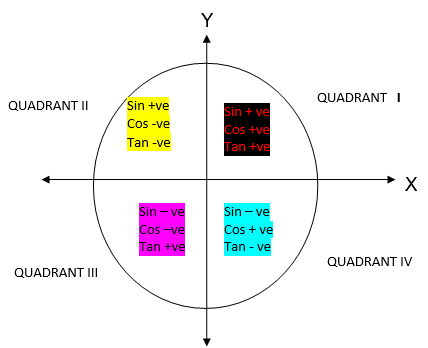
We have seen that trigonometrical ratios are positive or negative depending on the size of the angle and the quadrant in which it is found.

The result can be summarized by using the following diagram.

Trigonometric Ratios to Solve Problems in Daily Life

Apply trigonometric ratios to solve problems in daily life

Example 1

Write the signs of the following ratios

1. Sin 170⁰
2. Cos 240⁰
3. Tan 310⁰
4. sin 30⁰

Solution

a)Sin 170⁰

Since 170⁰ is in the second quadrant, then Sin 170⁰ = Sin (180⁰-170⁰) = Sin 10⁰

∴Sin 170⁰ = Sin 10⁰

b) Cos 240⁰ = -Cos (240⁰-180⁰⁾= -Cos 60⁰

Therefore Cos 240⁰= -Cos 60⁰

c) Tan 310⁰ = -Tan (360⁰-310⁰) = - Tan 50⁰

Therefore Tan 310⁰= -Tan 50⁰

d) Sin 300⁰= -sin (360⁰-300⁰) = -sin 60⁰

Therefore sin 300⁰= - Sin 60⁰

Relationship between Trigonometrical ratios

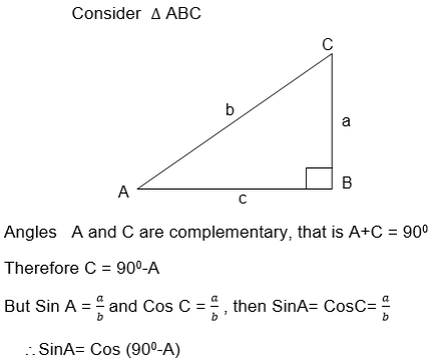
The above relationship shows that the Sine of angle is equal to the cosine of its complement.

Also from the triangle ABC above

Again using the ΔABC

b² = a²+c² (Pythagoras theorem)

And

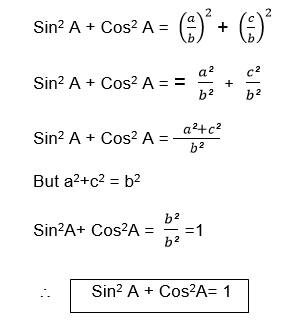
Example 2

Given thatA is an acute angle and Cos A= 0.8, find

1. Sin A
2. tan A.

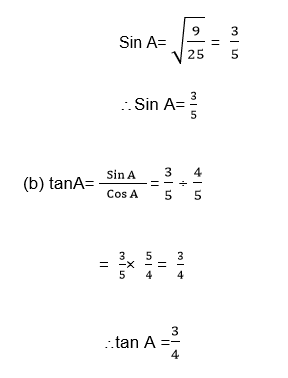
Example 3

If A and B are complementary angles,

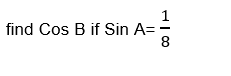
Solution

If A and B are complementary angle

Then Sin A = Cos B and Sin B = Cos A

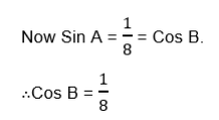
Example 4

Given that θand βare acute angles such that θ+ β= 90⁰ and Sinθ= 0.6, find tanβ

Solution

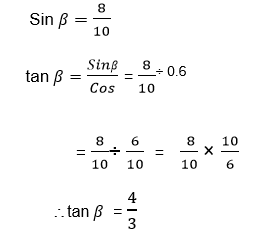
Exercise 1

For practice

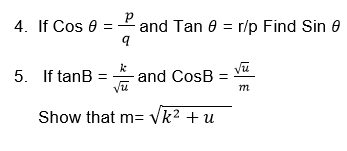
Sine and Cosine Functions

Sines and Cosines of Angles 0 Such That -720°≤ᶿ≥ 720°

Find sines and cosines of angles 0 such that -720°≤ᶿ≥ 720°

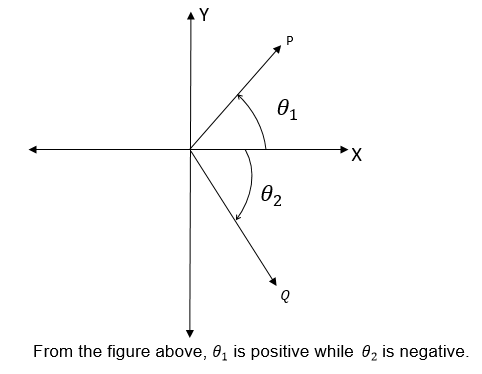
Positive and Negative angles

An angle can be either positive or negative.

Definition:

Positive angle: is an angle measures in anticlockwise direction from the positive X- axis

Negative angle: is an angle measured in clockwise direction from the positive X-axis

Facts:

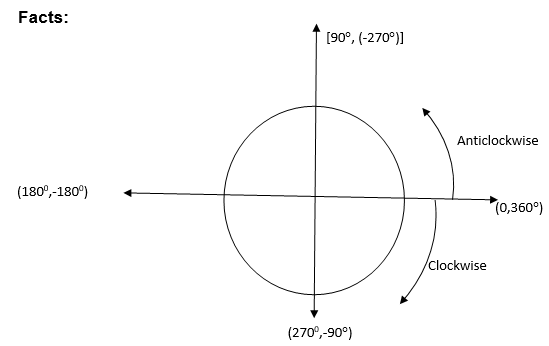
1. From the above figure if is a positive angle then the corresponding negative angle to is (- 360⁰) or (+ - 360⁰)
2. .If is a negative angle, its corresponding positive angle is (360+)

Example 5

Find thecorresponding negative angle to the angle θif ;

1. θ= 58⁰
2. θ= 245⁰

Example 6

What is the positive angle corresponding to - 46°?

SPECIAL ANGLES

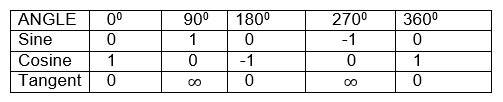
The angles included in this group are 0⁰, 30⁰, 45⁰, 60⁰, 90⁰, 180⁰, 270⁰, and 360⁰

Because the angle 0⁰, 90⁰, 180⁰, 270⁰, and 360⁰, lie on the axes then theirtrigonometrical ratios are summarized in the following table.

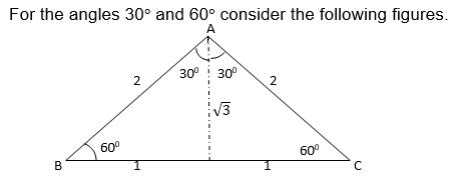
The ∆ ABC is an equilateral triangle of side 2 units

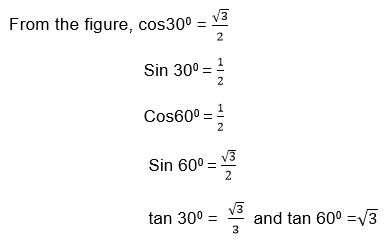
For the angle 45⁰ consider the following triangle

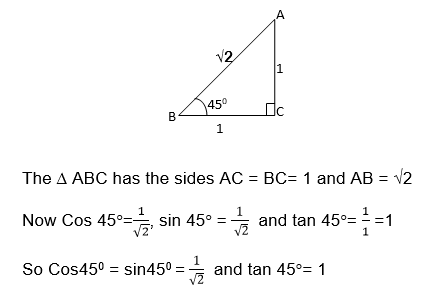
The following table summarizes the Cosine, Sine, and tangent of the angle 30⁰ , 45⁰ and 60⁰

NB: The following figure is helpful to remember the trigonometrical ratios of special angles from 0°to 90°

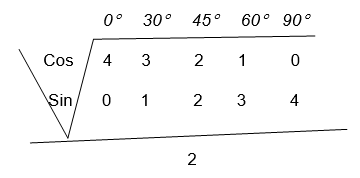
If we need the sines of the above given angles for examples, we only need to take the square root of the number below the given angle and then the result is divided by 2.

Example 7

Find the sine,cosine and tangents of each of the following angles

1. -135⁰
2. 120⁰
3. 330⁰

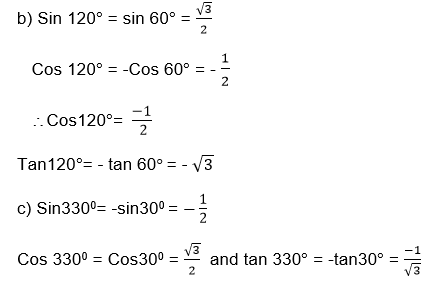
Example 8

Find the value of θif Cos θ= -½ and θ≤ θ≤ 360°

Solution

Since Cos θis – (ve), then θlies in either the second or third quadrants,

Now - Cos (180 –θ= - Cos (θ+180⁰) = -½= -Cos60⁰

So θ= 180⁰-60⁰ = 120⁰ or θ= 180⁰ + 60⁰ = 240⁰

θ= 120⁰ 0r θ=240⁰

Example 9

Consider below

Exercise 2

Solve the Following.

The Graphs of Sine and Cosine

Draw the graphs of sine and cosine

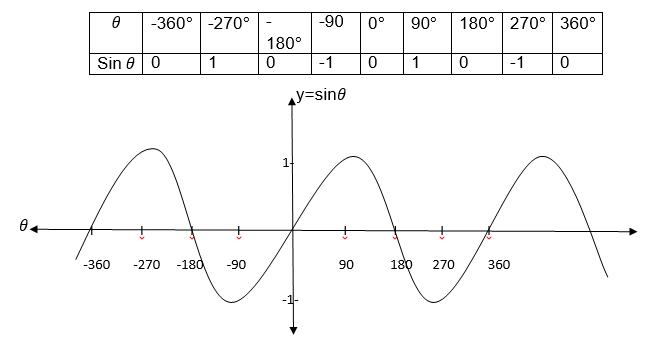
Consider the following table of value for y=sinθ where θranges from - 360°to 360°

For cosine consider the following table of values

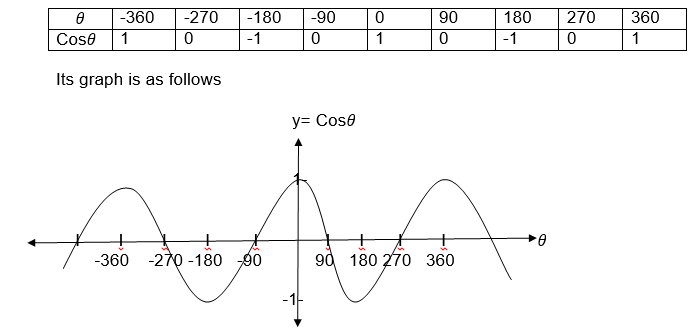
From the graphs for the two functions a reader can notice that sinθand cosθboth lie in the interval -1 and 1 inclusively, that is -1≤sinθ1 and -1≤cosθ≤1 for all values of θ.

The graph of y= tanθis left for the reader as an exercise

NB: -∞≤ tanθ≤∞the symbol ∞means infinite

Also you can observe that both Sinθnd cosθrepeat themselves at the interval of

360°, which means sinθ= sin(θ+360) = sin(θ+2x360⁰) etc

and Cosθ=(Cosθ+360⁰)= Cos(θ+2x360⁰)

Each of these functions is called a period function with a period 360⁰

1. Usingtrigonometrical graphs in the interval -360⁰≤θ≤360⁰

Find θsuch that

1. Sin= 0.4
2. Cos= 0.9

solution

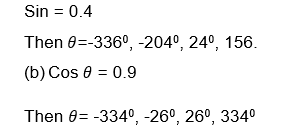
Example 10

Use the graph of sinθto find the value ofθif

4Sinθ= -1.8 and -360⁰ ≤θ≤360⁰

Solution

4Sinθ= -1.8

Sinθ= -1.8÷4 = -0.45

Sinθ= -0.45

So θ= -153⁰, -27⁰, 207⁰, 333⁰

The graphs of sine and cosine functions

Interpret the graphs of sine and cosine functions

Example 11

Use thetrigonometrical function graphs for sine and cosine to find the value of

1. Sin (-40⁰)
2. Cos (-40⁰)

Solution

1. Sin (-40⁰)= - 0.64
2. Cos (-40⁰)= 0.76

Sine and Cosine Rules

The Sine and Cosine Rules

Derive the sine and cosine rules

Consider the triangle ABC drawn on a coordinate plane

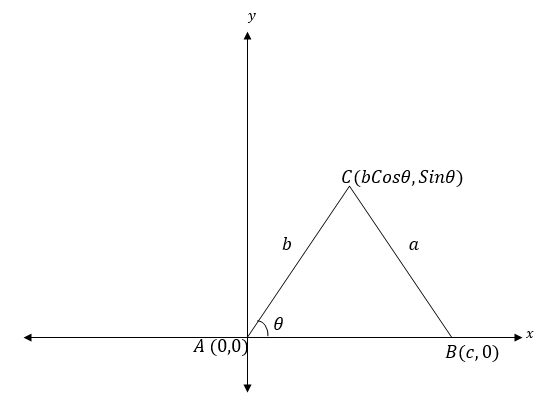
From the figure above the coordinates of A, B and C are (0, 0), (c, 0) and(bCosθ, bSinθ) respectively.

Now by using the distance formula

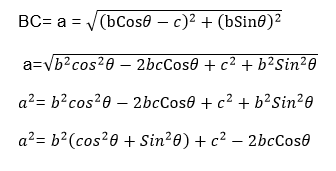
SINE RULE

Consider the triangle ABC below

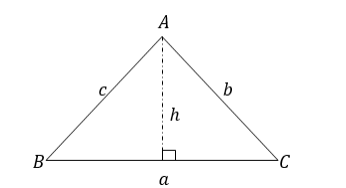
From the figure above,

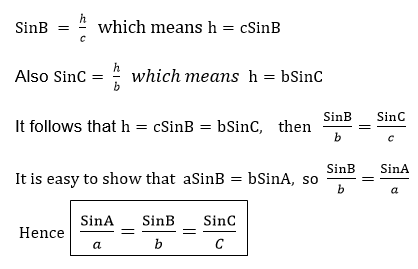
Note that this rule can be started as “In any triangle the side are proportional to the Sines of the opposite angles”

The Sine and Cosine Rules in Solving Problems on Triangles

Apply the sine and cosine rules in solving problems on triangles

Example 12

Find the unknown side and angle in a triangle ABC given that

a= 7.5cm

c= 8.6cm and C= 80°

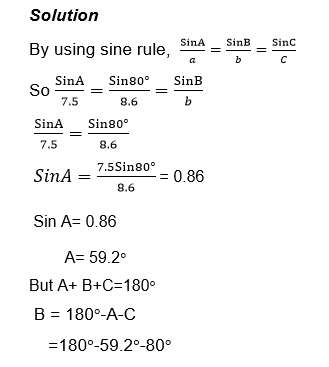
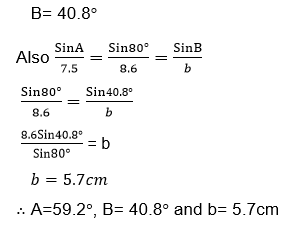
Find the unknown sides and angle in a triangle ABC in which a= 22.2cmB= 86°and A= 26°

Solution

By sine rule

Sin A= sin B= Sin C

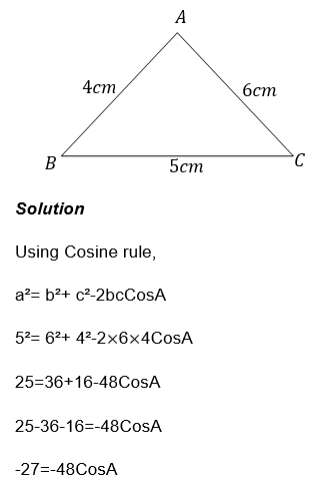
Example 13

Find unknown sides and angles in triangle ABC

Where a=3cm, c= 4cm and B= 30°

Solution

By cosine rule,

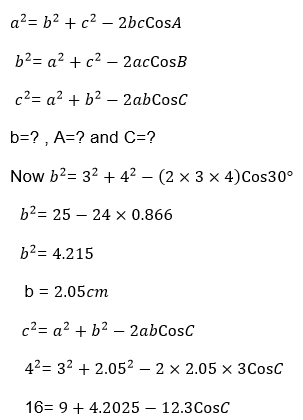
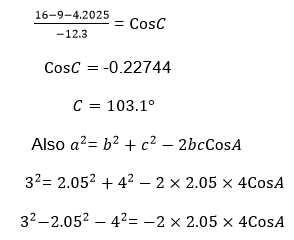
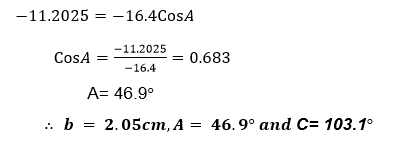
Example 14

Find the unknown angles in the following triangle

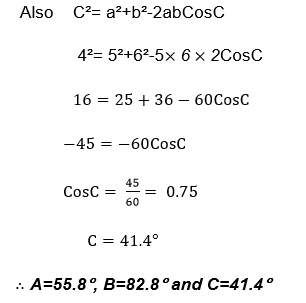
Exercise 3

1. Given thata=11cm, b=14cm and c=21cm, Find the Largest angle of ΔABC

2. If ABCD is a parallelogram whose sides are 12cm and 16cm what is the length of the diagonal AC if angle B=119°?

3. A and B are two ports on a straight Coast line such that B is 53km east of A. A ship starting from A sails 40km to a point C in a direction E65°N. Find:

1. The distance a of the ship from B
2. The distance of the ship from the coast line.

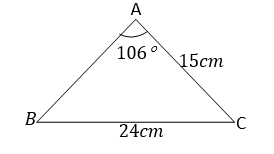
4. Find the unknown angles and sides in the following triangle.

5. <!--[endif]-->A rhombus has sides of length 16cm and one of its diagonals is 19cm long. Find the angles of the rhombus.

Compound Angles

The Compound of Angle Formulae or Sine, Cosine and Tangent in Solving Trigonometric Problems

Apply the compound of angle formulae or sine, cosine and tangent in solving trigonometric problems

The aim is to express Sin (α±β) and Cos (α±β) in terms of Sinα, Sinβ, Cosαand Cosβ

Consider the following diagram:

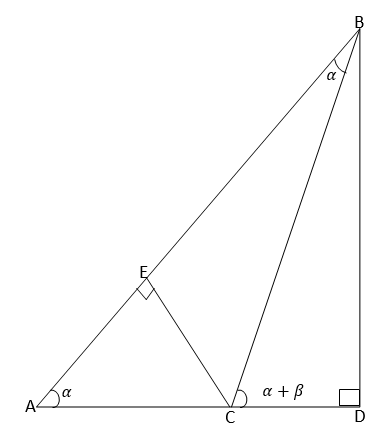
From the figure above <BAD=αand <ABC=βthus<BCD=α+β

From ΔBCD

For Cos(α±β) Consider the following unit circle with points P and Q on it such that OP,makes angleα with positive x-axis and OQ makes angle βwith positive x-axes.

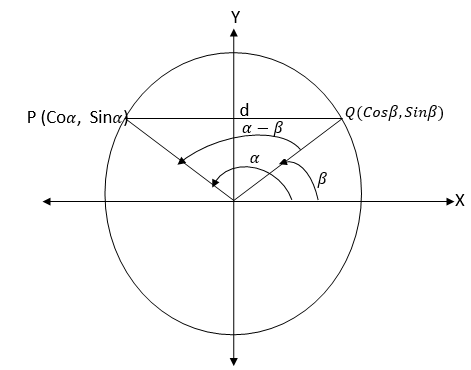
From the figure above the distance d is given by

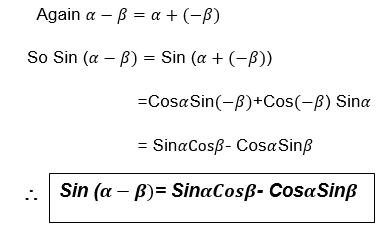
In general

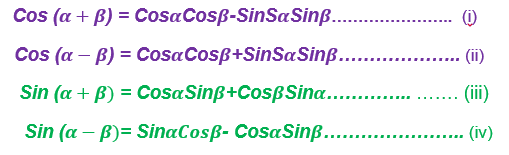
Example 15

1. Withoutusing tables find the value of each of the following:

1. Sin 75°
2. Cos105

Solution:

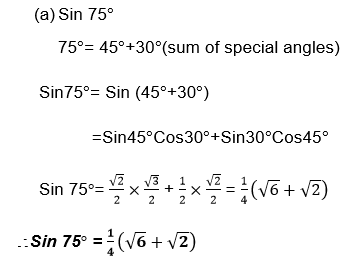
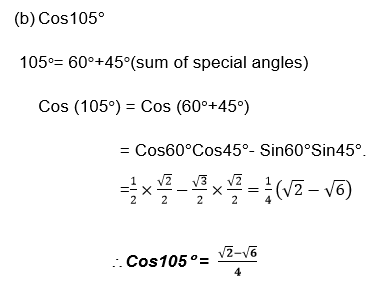
Example 16

Find:

1. Sin150°
2. Cos 15°

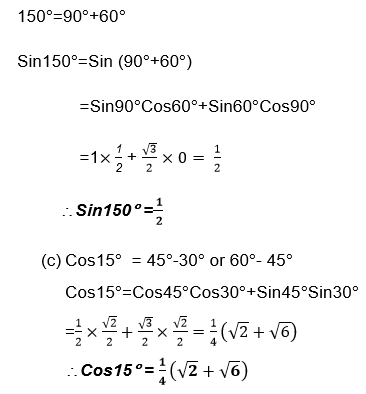
Exercise 4

1. Withoutusing tables, find:

1. Sin15°
2. Cos 120°

2. FindSin 225° from (180°+45°)

3. <!--[endif]-->Verify that

1. Sin90° = 1 by using the fact that 90°=45°+45°
2. Cos90°=0 by using the fact that 90°=30°+60°

4. <!--[endif]-->Express each of the following in terms of sine, cosine and tangent of acute angles.

1. Sin107°
2. Cos300°

5. <!--[endif]-->By using the formula for Sin (A-B), show that Sin (90°-C)=Cos C