Join Our Groups
TOPIC 1: COORDINATE GEOMETRY
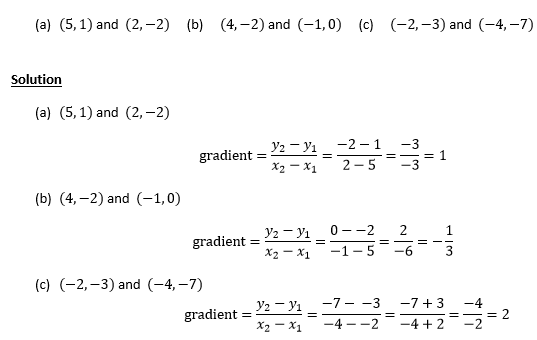
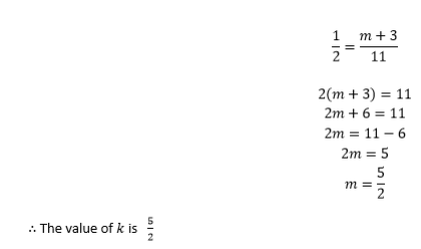
FINDING THE EQUATION OF A STRAIGHT LINE
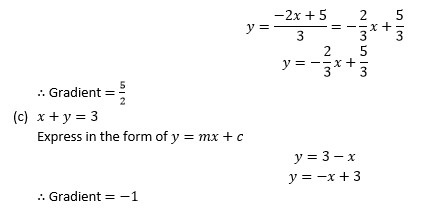
GRAPHS OF STRAIGHT LINES
The General Equation of a Straight Line
Derive the general equation of a straight line
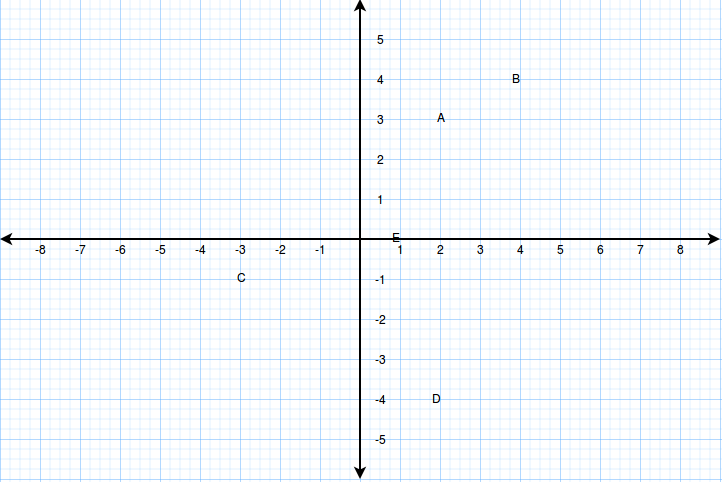
COORDINATES OF A POINT
•The coordinates of a points - are the values of x and y enclosed by the brackets which are used to describe the position of point in a line in the plane.
The plane is called xy-plane and it has two axis.
- horizontal axis known as axis and
- vertical axis known as axis
Consider the xy-plane below
The coordinates of points A, B, C ,D and E are A(2, 3), B(4, 4), C(-3, -1), D(2, -4) and E(1, 0).
Definition
Example 1
Find the gradient of the lines joining
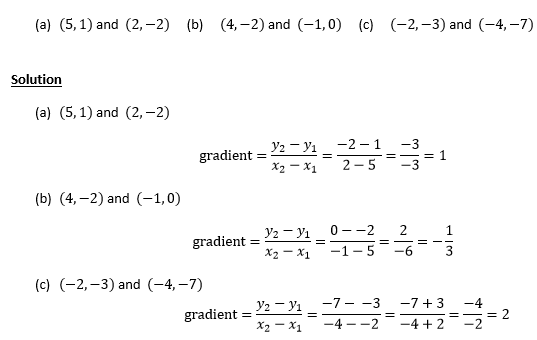
Example 2
(a) The line joining (2, -3) and (k, 5) has a gradient -2. Find k
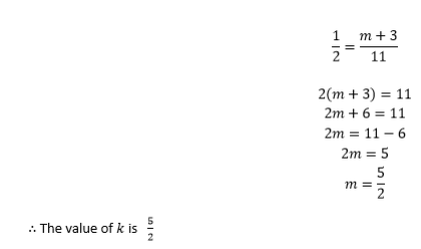
Exercise 1
1. Find the gradientof the line which passes through the following points ;
- (3,6) and (-2,8)
- (0,6) and (99,-12)
- (4,5)and (5,4)
2. A line passes through (3, a) and (4, -2), what is the value of a if the slope of the line is 4?
3. The gradient of the linewhich goes through (4,3) and (-5,k) is 2. Find the value of k.
FINDING THE EQUATION OF A STRAIGHT LINE
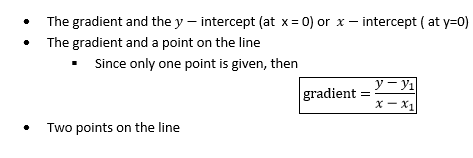
The equation of a straight line can be determined if one of the following is given:-
Example 3
Find the equation of the line with the following
- Gradient 2 and y-intercept -4
- Gradient -2/3 and passing through the point (2,4)
- A line passing through the point (3,4) and (4,5)
Solution
EQUATION OF A STRAIGHT LINE IN DIFFERENT FORMS
The equation of a line can be expressed in two forms
Example 4
Find the gradient of the following lines
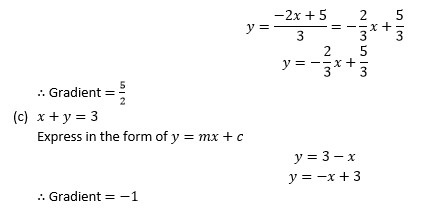
INTERCEPTS
Therefore
Example 5
Find the y-intercept of the following lines
Example 6
Find the x and y-intercept of the following lines
Exercise 2
Attempt the following Questions.
- Find the y-intercept of the line 3x+2y = 18 .
- What is the x-intercept of the line passing through (3,3) and (-4,9)?
- Calculate the slope of the line given by the equation x-3y= 9
- Find the equation of the straight line with a slope -4 and passing through the point (0,0).
- Find the equation of the straight line with y-intercept 5 and passing through the point (-4,8).
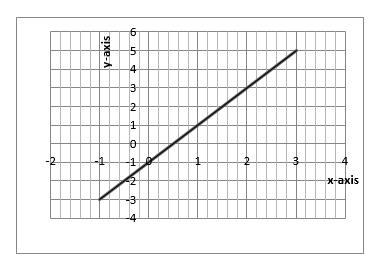
GRAPHS OF STRAIGHT LINES
The graph of straight line can be drawn by using the following methods;
- By using intercepts
- By using the table of values
Example 7
Sketch the graph of Y = 2X - 1
SOLVING SIMULTANEOUS EQUATION BY GRAPHICAL METHOD
- Use the intercepts to plot the straight lines of the simultaneous equations
- The point where the two lines cross each other is the solution to the simultaneous equations
Example 8
Solve the following simultaneous equations by graphical method
Exercise 3
1. Draw the line 4x-2y=7 and 3x+y=7 on the same axis and hence determine their intersection point
2. Find the solutionfor each pair the following simultaneous equations by graphical method;
- y-x = 3 and 2x+y = 9
- 3x- 4y=-1 and x+y = 2
- x = 8 and 2x-3y = 10
The Coordinates of the Midpoint of a Line Segment
Determine the coordinates of the midpoint of a line segment
Let S be a point with coordinates (x1,y1), T with coordinates (x2,y2) and M with coordinates (x,y) where M is the mid-point of ST. Consider the figure below:
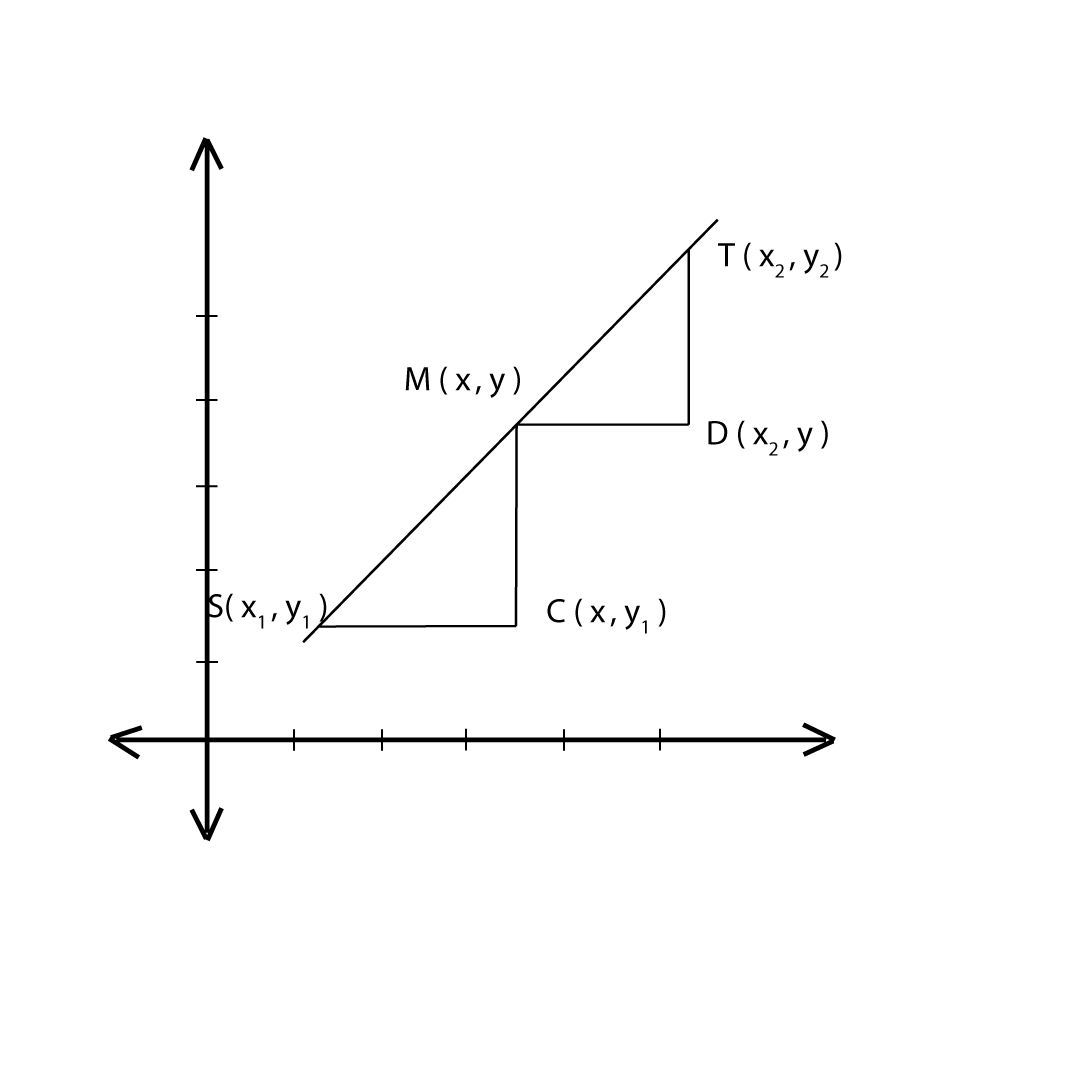
Considering the angles of the triangles SMC and TMD, the triangles SMC and TMD are similar since their equiangular
Example 9
Find the coordinates of the mid-point joining the points (-2,8) and (-4,-2)
Solution
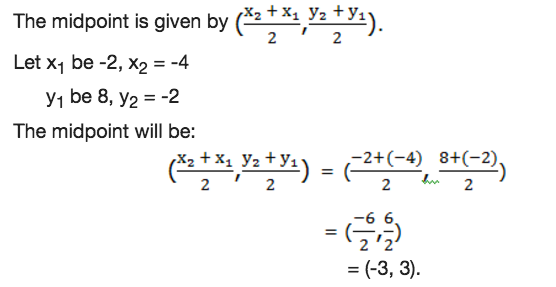
Therefore the coordinates of the midpoint of the line joining the points (-2,8) and (-4, -2) is (-3,3).
The Distance Between Two Points on a Plane
Calculate the distance between two points on a plane
Consider two points, A(x1,y1) and B(x2,y2) as shown in the figure below:
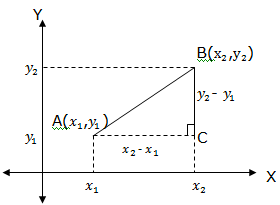
The distance between A and B in terms of x1, y1,x2, and y2can be found as follows:Join AB and draw doted lines as shown in the figure above.
Then, AC = x2– x1and BC = y2– y1
Since the triangle ABC is a right angled, then by applying Pythagoras theorem to the triangle ABC we obtain
Therefore the distance is 13 units.
Gradients in order to Determine the Conditions for any Two Lines to be Parallel
Compute gradients in order to determine the conditions for any two lines to be parallel
The two lines which never meet when produced infinitely are called parallel lines. See figure below:
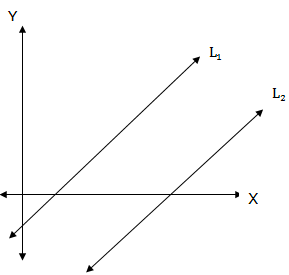
The two parallel lines must have the same slope. That is, if M1is the slope for L1and M2is the slope for L2thenM1= M2
Gradients in order to Determine the Conditions for any Two Lines to be Perpendicular
Compute gradients in order to determine the conditions for any two lines to be perpendicular
When two straight lines intersect at right angle, we say that the lines are perpendicular lines. See an illustration below.
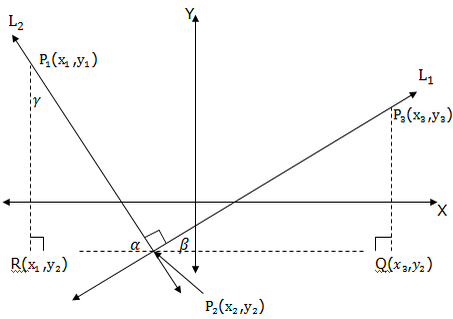
Consider the points P1(x1,y1), P2(x2,y2), P3(x3,y3), R(x1,y2) and Q(x3,y2) and the anglesα,β,γ(alpha, beta and gamma respectively).
- α+β = 90 (complementary angles)
- α+γ= 90 (complementary angles)
- β = γ (alternate interior angles)
Therefore the triangle P2QP3is similar to triangle P1RP2.
Generally two perpendicular lines L1and L2with slopes M1and M2respectively the product of their slopes is equal to negative one. That is M1M2= -1.
Example 10
Show that A(-3,1), B(1,2), C(0,-1) and D(-4,-2) are vertices of a parallelogram.
Solution
Let us find the slope of the lines AB, DC, AD and BC
We see that each two opposite sides of the parallelogram have equal slope. This means that the two opposite sides are parallel to each other, which is the distinctive feature of the parallelogram. Therefore the given vertices are the vertices of a parallelogram.
Problems on Parallel and Perpendicular Lines
Solve problems on parallel and perpendicular lines
Example 11
Show that A(-3,2), B(5,6) and C(7,2) are vertices of a right angled triangle.
Solution
Right angled triangle has two sides that are perpendicular, they form 90°.We know that the slope of the line is given by: slope = change in y/change in x
Now,
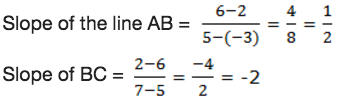
Since the slope of AB and BC are negative reciprocals, then the triangle ABC is a right angled triangle at B.
Well arranged and understandable notes! Thank you!
ReplyDelete